
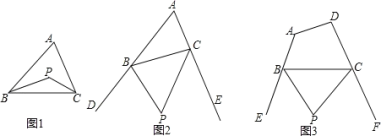
【题目】(1)探究1:如图1,P是△ABC的内角∠ABC与∠ACB的平分线BP和CP的交点,若∠A=70,则∠BPC=_______度;
(2)探究2:如图2,P是△ABC的外角∠DBC与外角∠ECB的平分线BP和CP的交点,求∠BPC与∠A的数量关系?并说明理由。
(3)拓展:如图3,P是四边形ABCD的外角∠EBC与∠BCF的平分线BP和CP的交点,设∠A+∠D=α.,直接写出∠BPC与α的数量关系;
【答案】(1)125°;(2)∠BPC=90°﹣![]() ∠A,理由见解析;(3)∠BPC =180°﹣
∠A,理由见解析;(3)∠BPC =180°﹣![]()
【解析】
(1)借助角平分线的性质即可得到∠PBC=![]() ∠ABC以及∠PCB=
∠ABC以及∠PCB=![]() ∠ACB,然后在△BPC中进一步分析可找出∠BPC与∠A的关系,进而求出∠BPC的度数;
∠ACB,然后在△BPC中进一步分析可找出∠BPC与∠A的关系,进而求出∠BPC的度数;
(2)根据三角形内角和定理可知∠BPC=180°﹣(∠PBC+∠PCB),根据角平分线的定义可用![]() (∠DBC+∠ECB)表示∠PBC+∠PCB,再利用三角形外角性质得到∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC,即可求出∠BPC与∠A的关系;
(∠DBC+∠ECB)表示∠PBC+∠PCB,再利用三角形外角性质得到∠DBC+∠ECB=∠A+∠ACB+∠A+∠ABC,即可求出∠BPC与∠A的关系;
(3)延长BA、CD相交于点Q,由(2)的分析可直接得出∠P与∠Q的关系,而∠BAD与∠CDA是△ADQ的外角,再结合三角形外角性质即可解答.
(1)解:∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣![]() (∠ABC+∠ACB)
(∠ABC+∠ACB)
=180°﹣![]() (180°﹣∠A)
(180°﹣∠A)
=90°+![]() ∠A
∠A
=90°+35°
=125°
故答案为:125°
(2)∠BPC=90°﹣![]() ∠A
∠A
理由如下:
∠BPC=180°﹣(∠PBC+∠PCB)
=180°﹣![]() (∠DBC+∠ECB)
(∠DBC+∠ECB)
=180°﹣![]() (∠A+∠ACB+∠A+∠ABC)
(∠A+∠ACB+∠A+∠ABC)
=180°﹣![]() (∠A+180°)
(∠A+180°)
=90°﹣![]() ∠A
∠A
(3)延长BA、CD相交于点Q,如图
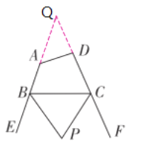
∠BPC=90°﹣![]() ∠Q
∠Q
∴∠Q=180°﹣2∠BPC
∴∠BAD+∠CDA=180°+∠Q=180°+180°﹣2∠BPC =360°﹣2∠BPC
∴∠BPC =180°﹣![]()
故答案为:∠BPC =180°﹣![]()


科目:初中数学 来源: 题型:
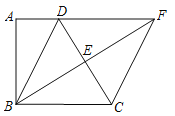
【题目】如图,四边形ABCD中,AD∥BC,∠A=90°,BD=BC,点E为CD的中点,射线BE交AD的延长线于点F,连接CF.
(1)求证:四边形BCFD是菱形;
(2)若AD=1,BC=2,求BF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将函数y=![]() (x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )
(x﹣2)2+1的图象沿y轴向上平移得到一条新函数的图象,其中点A(1,m),B(4,n)平移后的对应点分别为点A'、B'.若曲线段AB扫过的面积为9(图中的阴影部分),则新图象的函数表达式是( )

A. ![]() B.
B. ![]()
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】小亮同学为了巩固自己对平行四边形判定知识的掌握情况,设计了一个游戏,他将四边形ABCD中的部分条件分别写在四张大小、质地及背面颜色都相同的卡片上,卡片如图,他将卡片正面朝下反扣在桌面上,洗匀后从中随机抽取两张,然后根据卡片上的两个条件判断四边形ABCD是否为平行四边形,请你用列举法(列表法或树状图法)求出他能够判定四边形ABCD为平行四边形的概率.(卡片可用a、b、c、d表示)

查看答案和解析>>
科目:初中数学 来源: 题型:
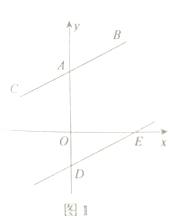
【题目】已知,点![]() ,点
,点![]() 分别在
分别在![]() 轴正半轴和负半轴上,
轴正半轴和负半轴上,![]() .
.
(1)如图1,若![]() ,
,![]() ,求
,求![]() 的度数;
的度数;
(2)在![]() 和
和![]() 内作射线
内作射线![]() ,
,![]() ,分别与过
,分别与过![]() 点的直线交于第一象限内的点
点的直线交于第一象限内的点![]() 和第三象限内的点
和第三象限内的点![]() .
.
①如图2,若![]() ,
,![]() 恰好分别平分
恰好分别平分![]() 和
和![]() ,求
,求![]() 的值;
的值;
②若![]() ,
,![]() ,当
,当![]() ,则
,则![]() 的取值范围是__________.
的取值范围是__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等边三角形,
是等边三角形,![]() 是
是![]() 上一点,
上一点,![]() 绕点
绕点![]() 逆时针旋转到
逆时针旋转到![]() 的位置.
的位置.
(1)如图,旋转中心是 ,![]() ;
;
(2)如图,如果![]() 是
是![]() 的中点,那么经过上述旋转后,点
的中点,那么经过上述旋转后,点 ![]() 转动了 度;
转动了 度;
(3)如果点![]() 为
为![]() 边上的三等分点,且
边上的三等分点,且![]() 的面积为
的面积为![]() ,那么四边形
,那么四边形![]() 的面积为 .
的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BD为□ABCD的对角线,按要求完成下列各题.

(1)用直尺和圆规作出对角线BD的垂直平分线交AD于点E,交BC于点F,垂足为O.(保留作图痕迹,不要求写作法)
(2)在(1)的基础上,连接BE和DF.求证:四边形BFDE是菱形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】探究与发现:在△ABC中,∠B=∠C,点D在BC边上(点B、C除外),点E在AC边上,且∠ADE=∠AED,连接DE.
(1)如图①,若∠B=∠C=45,
①当∠BAD=60时,求∠CDE的度数;
②试猜想∠BAD与∠CDE的数量关系,并说明理由.
(2)深入探究:如图②,若∠B=∠C,但∠C≠45,其他条件不变,试探究∠BAD与∠CDE的数量关系.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形 ABCD 中,AB=2,∠DAB=60°,点 E 是 AD 边的中点,点 M 是 AB 边上的一个动点(不与点 A 重合), 延长 ME 交 CD 的延长线于点 N,连接MD,AN.

(1)求证:四边形 AMDN 是平行四边形.
(2)当 AM 的值为何值时,四边形 AMDN 是矩形?请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com