
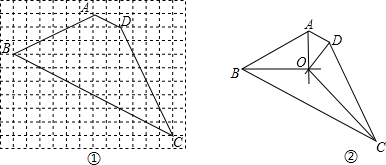
解:(1)如图:AO,BO为∠A、∠B的平分线,
(2)如(1)中图,
∵在△EOC和△FOC中,

,
∴△EOC≌△FOC(SSS),
∴∠ECO=∠FCO,
∴O点在∠BCD的角平分线上,
同理:O点也在∠ADC的角平分线上,
(3)如图:OA⊥BO,
∴∠OAB+∠OBA=90°,
∵AO,BO为∠A、∠B的平分线,
∴∠BAD+∠CBA=180°,
∴AD∥BC,
∴∠ADC+∠BCD=180°,
∵OD,OC分别为∠DCB,∠CDA的角平分线,
∴∠ODC+∠OCD=90°,
∴OD⊥OC,
∴∠AOD+∠BOC=180°,
∵O点为四边形四个内角的角平分线的交点,
∴O点为其内心,
∴AD+BC=AB+CD,
∵AB≠CD,
∴S
△AOB≠S
△COD,
(4)∵四边形ABCD中四个内角平分线仍相交于一点O,
∴O点为四边形ABCD的内心,
∴AD+BC=AB+CD,
∴在(3)的正确结论中,③仍然成立.
故答案为①②③⑤.
分析:(1)利用网格线很容易作出∠A、∠B的平分线,
(2)结合图形,通过求证三角形全等,即可推出点O在其他两个角的平分线上,(3)根据(1)(2)中所推出的结论,可知OA⊥BO,结合角平分线的性质,即可推出结论①和②,再根据周角的定义,即可推出结论⑤,然后根据四边形内切圆的定义和性质,即可推出结论③,(4)根据图2,只能推出O点为四边形的内心,既而得出结论③AD+BC=AB+CD.
点评:本题主要考查角平分线的性质、作角平分线,全等三角形的判定与性质、四边形的内切圆的定义与性质等知识点,关键在于结合网络图形分析出相等关系,熟练正确地运用相关的性质定理.

 解:(1)如图:AO,BO为∠A、∠B的平分线,
解:(1)如图:AO,BO为∠A、∠B的平分线, ,
,

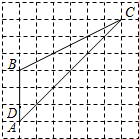 如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=
如图,在正方形网格中,点A、B、C、D都是格点,点E是线段AC上任意一点.如果AD=1,那么当AE=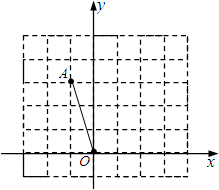 如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).
如图,在正方形网格中建立平面直角坐标系,格点O为原点,格点A的坐标为(-1,3).