
【题目】如图,已知△ABC和△ADE均为等边三角形,BD、CE交于点F.
(1)求证:BD=CE;(2)求锐角∠BFC的度数.
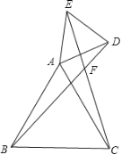
【答案】(1)证明见解析;(2)∠BFC=60°.
【解析】
(1)根据等边三角形的性质得出AE=AD,再由∠EAD+∠DAC=∠BAC+∠DAC,得出∠DAB=∠EAC,利用SAS可证得△EAC≌△DAB,从而可得出结论.
(2)根据△EAC≌△DAB可得∠ECA=∠DAB,从而在△BFC中可得∠ECA+∠FBC=60°,结合∠ACB=60°,利用三角形的内角和定理可得出∠BFC的度数.
(1)证明:∵△ABC和△ADE均为等边三角形,
∴AE=AD、AB=AC,
又∵∠EAD=∠BAC=60°,∠EAD+∠DAC=∠BAC+∠DAC,即∠DAB=∠EAC,
在△EAC和△DAB中,
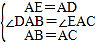 ,
,
∴△EAC≌△DAB,
即可得出BD=CE.
(2)由(1)△EAC≌△DAB,可得∠ECA=∠DBA,
又∵∠DBA+∠DBC=60°,
在△BFC中,∠ECA+∠DBC=60°,∠ACB=60°,
则∠BFC=180°-∠ACB-(∠ECA+∠DBC)=180°-60°-60°=60°.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】在![]() 中,
中,![]() 为直线
为直线![]() 上一点,
上一点,![]() 为直线
为直线![]() 上一点,
上一点,![]()


(1)如图1,当![]() 在
在![]() 上,
上,![]() 在
在![]() 上时,求证
上时,求证![]() ;
;
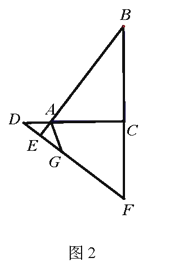
(2)如图2,当![]() 在
在![]() 的延长线上,
的延长线上,![]() 在
在![]() 的延长线上时,点
的延长线上时,点![]() 在
在![]() 上,连接
上,连接![]() ,且
,且![]() ,求证:
,求证:![]()
(3)如图3,在(2)的条件下,连接![]() 当
当![]() 平分
平分![]() 时,将
时,将![]() 沿着
沿着![]() 折至
折至![]() 探究
探究![]() 与
与![]() 的数量关系.
的数量关系.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AC=BC,D是BC上的一点,且满足∠BAD= ![]() ∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
∠C,以AD为直径的⊙O与AB,AC分别相交于点E,F.
(1)求证:直线BC是⊙O的切线;
(2)连接EF,若tan∠AEF= ![]() ,AD=4,求BD的长.
,AD=4,求BD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
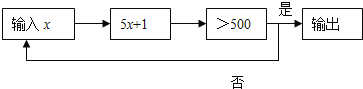
【题目】按下面程序计算,即根据输入的![]() 判断
判断![]() 是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的
是否大于500,若大于500则输出,结束计算,若不大于500,则以现在的![]() 的值作为新的
的值作为新的![]() 的值,继续运算,循环往复,直至输出结果为止.若开始输入
的值,继续运算,循环往复,直至输出结果为止.若开始输入![]() 的值为正整数,最后输出的结果为656,则满足条件的所有
的值为正整数,最后输出的结果为656,则满足条件的所有![]() 的值是__.
的值是__.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C为⊙O上一点,AD和过C点的直线互相垂直,垂足为D,且AC平分∠DAB.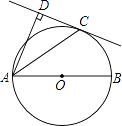
(1)求证:DC为⊙O的切线;
(2)若⊙O的半径为5,BC=6,求CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ACDE是证明勾股定理时用到的一个图形,a、b、c是Rt△ABC和Rt△BED边长,易知AE=![]() c,这时我们把关于x的形如ax+
c,这时我们把关于x的形如ax+![]() cx+b=0的一元二次方程称为“勾系一元二次方程”.
cx+b=0的一元二次方程称为“勾系一元二次方程”.

请解决下列问题:
写出一个“勾系一元二次方程”;
求证:关于x的“勾系一元二次方程”ax+![]() cx+b=0必有实数根;
cx+b=0必有实数根;
若x=1是“勾系一元二次方程”ax+![]() cx+b=0的一个根,且四边形ACDE的周长是
cx+b=0的一个根,且四边形ACDE的周长是![]() ,求△ABC面积.
,求△ABC面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
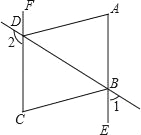
【题目】如图,∠1+∠2=180°,∠A=∠C,DA平分∠BDF.
(1)AE与FC会平行吗?说明理由;
(2)AD与BC的位置关系如何?为什么?
(3)BC平分∠DBE吗?为什么.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,点A、B、C在同一条直线上,点M为线段AC的中点、点N为线段BC的中点.
(1)如图,当点C在线段AB上时:
①若线段![]() ,求
,求![]() 的长度.
的长度.
②若AB=a,求MN的长度.
(2)若![]() ,求MN的长度(用含
,求MN的长度(用含![]() 的代数式表示).
的代数式表示).
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在正方形ABCD中,对角线AC,BD交于点O,点P在线段BC上(不含点B),∠BPE= ![]() ∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.
∠ACB,PE交BO于点E,过点B作BF⊥PE,垂足为F,交AC于点G.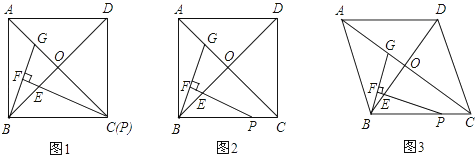
(1)当点P与点C重合时(如图①),求证:△BOG≌△POE;
(2)结合图②,通过观察、测量、猜想: ![]() 与
与 ![]() 的关系,并证明你的猜想;
的关系,并证明你的猜想;
(3)把正方形ABCD改为菱形,其他条件不变(如图③),若AC=8,BD=6,直接写出 ![]() 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com