
【题目】阅读与理解:
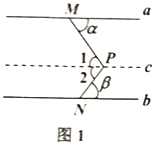
如图1,直线![]() ,点P在a,b之间,M,N分别为a,b上的点,P,M,N三点不在同一直线上,PM与a的央角为
,点P在a,b之间,M,N分别为a,b上的点,P,M,N三点不在同一直线上,PM与a的央角为![]() ,PN与b的夹角为
,PN与b的夹角为![]() ,则
,则![]() .
.
理由如下:
过P点作直线![]() ,因为
,因为![]() ,所以
,所以![]() (如果两条直线都与第三条直线平行,那么这两条直线也互相平行).所以
(如果两条直线都与第三条直线平行,那么这两条直线也互相平行).所以![]() ,
,![]() .(两直线平行,内错角相等),所以
.(两直线平行,内错角相等),所以![]() ,即
,即![]() .
.
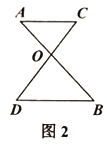
计算与说明:
已知:如图2,AB与CD交于点O.
(1).若![]() ,求证:
,求证:![]() ;
;
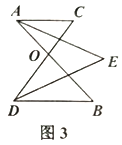
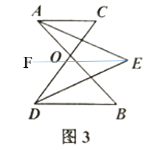
(2)2.如图3,已知![]() ,AE平分
,AE平分![]() ,DE平分
,DE平分![]() .
.
①若![]() ,
,![]() ,请你求出
,请你求出![]() 的度数;
的度数;
②请问:图3中,![]() 与
与![]() 有怎样的数量关系?为什么?
有怎样的数量关系?为什么?
【答案】(1)证明见解析;(2). ![]() ;(3)
;(3)![]() .理由见解析
.理由见解析
【解析】
(1)根据平行线的判定与性质即可证明;(2)①过E点作FE∥AC,即FE∥AC∥BD,根据已知条件求出∠EDB与∠CAE,再根据阅读材料得出∠E=∠EDB+∠CAE,即可进行求解;②根据外角定理知∠BOC=∠BAC+∠C,由平行的性质得出∠E=∠EDB+∠CAE=![]() ∠CDB+
∠CDB+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ∠BOC.
∠BOC.
(1)∵![]() ,
,
∴AC∥BD,
∴![]()
(2)①∵![]() ,∴AC∥BD,
,∴AC∥BD,
过E点作FE∥AC,即FE∥AC∥BD,
∵AE平分![]() ,
,![]() ,∴∠CAE=
,∴∠CAE=![]()
![]() =25°,
=25°,
∵![]() ,∴∠CDB=60°,∵DE平分
,∴∠CDB=60°,∵DE平分![]() , ∴∠BDE=
, ∴∠BDE=![]()
![]() =30°,
=30°,
由阅读材料得∠E=∠EDB+∠CAE=25°+30°=55°;
②![]() ,理由如下:
,理由如下:
∵∠BOC是△ACO的一个外角
∴∠BOC=∠BAC+∠C,
∵ FE∥AC∥BD,
∴∠C=∠CDB
∴∠E=∠EDB+∠CAE=![]() ∠CDB+
∠CDB+![]() ∠BAC=
∠BAC=![]() (∠BAC+∠C)=
(∠BAC+∠C)=![]() ∠BOC.
∠BOC.
即![]()


科目:初中数学 来源: 题型:
【题目】如图,是根据某市2014年至2018年工业生产总值绘制的折线统计图,观察统计图获得以下信息,其中判断错误的是( )
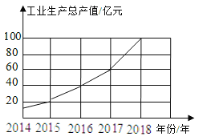
A.2014年至2018年工业生产总值逐年增加
B.2018年的工业生产总值比前一年增加了![]() 亿元
亿元
C.2016年与2017年每一年与前一年比,其增长额相同
D.2015年至2018年,每一年与前一年比,2018年的增长率最大
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB为⊙O的直径,C、D是⊙O上的点,且OC∥BD,AD分别与BC、OC相交于 点E、F.若∠CBD=36°,则下列结论中不正确的是
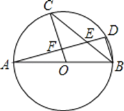
A. ∠AOC=72° B. ∠AEC=72° C. AF=DF D. BD=20F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,点D在AB上,点E在AC上,BE、CD相交于点O.
(1)若∠A=50°,∠BOD=70°,∠C=30°,求∠B的度数;
(2)试猜想∠BOC与∠A+∠B+∠C之间的关系,并证明你猜想的正确性.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在△ABC中,AB=AC,点D是直线BC上一点(不与B、C重合),以AD为一边在AD的右侧作△ADE,使AD=AE,∠DAE =∠BAC,连接CE.
(1)如图1,当点D在线段BC上,如果∠BAC=90°,则∠BCE=________度;
(2)设![]() ,
,![]() .
.
①如图2,当点在线段BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请说明理由;
之间有怎样的数量关系?请说明理由;
②当点在直线BC上移动,则![]() ,
,![]() 之间有怎样的数量关系?请直接写出你的结论.
之间有怎样的数量关系?请直接写出你的结论.




查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴的单位长度为1.
![]()
(1)如果点A,D表示的数互为相反数,那么点B表示的数是多少?
(2)如果点B,D表示的数互为相反数,那么图中表示的四个点中,哪一点表示的数的绝对值最大?为什么?
(3)当点B为原点时,若存在一点M到A的距离是点M到D的距离的2倍,则点M所表示的数是____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点 E、F分别为边 AD、CD上的动点(都与菱形的顶点不重合),联结 EF、BE、BF .
(1)若∠A=60°,且 AE+CF=AB,判断△BEF 的形状,并说明理由;
(2)在(1)的条件下,设菱形的边长为a,求△BEF面积的最小值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着手机的普及,微信![]() 一种聊天软件
一种聊天软件![]() 的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况
的兴起,许多人抓住这种机会,做起了“微商”,很多农产品也改变了原来的销售模式,实行了网上销售,这不刚大学毕业的小明把自家的冬枣产品也放到了网上,他原计划每天卖100斤冬枣,但由于种种原因,实际每天的销售量与计划量相比有出入,下表是某周的销售情况![]() 超额记为正,不足记为负
超额记为正,不足记为负![]() 单位:斤
单位:斤![]() ;
;
星期 | 一 | 二 | 三 | 四 | 五 | 六 | 日 |
与计划量的差值 |
|
|
|
|
|
|
|
(1)根据记录的数据可知前三天共卖出 ______ 斤;
(2)根据记录的数据可知销售量最多的一天比销售量最少的一天多销售 ______ 斤;
(3)本周实际销售总量达到了计划数量没有?
(4)若冬季每斤按8元出售,每斤冬枣的运费平均3元,那么小明本周一共收入多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com