【答案】
分析:(1)根据题意得到三角形ABD为等腰直角三角形,三角形ABC为含30°的直角三角形,根据题中的新定义,利用特殊角的加减即可得到∠DAC=∠DBC=15°,∠AED=∠BEC=75°,∠CED=∠AEB=105°;
(2)过E作EF于AB垂直,令AD=BD=a,设EF=x,在直角三角形ABD中,根据勾股定理表示出AB的长,判定出三角形BEF为等腰直角三角形,得到EF=BF=x,根据30度角的正切值,由EF=x,表示出AF的长,由AF+FB=AB列出等式,用含a的式子表示出x,根据30度角所对的直角边等于斜边的一半,求出AE=2x,表示出AE,用DB-BE表示出DE,在直角三角形ADE中,由正弦函数的定义:对边比斜边即DE比AE即可求出sin15°的值;
(3)根据题意画出图形,由直角三角形斜边上的中线等于斜边的一半得到点A,D,B,C
1,C
2都在以AB为直径的圆上,根据同弧所对的圆周角都相等得到∠ADC
2=∠ABC
2=∠BAC
1=30°,∠DAB=∠DBA=∠CC
1A=45°,然后由两对对应角相等的两三角形相似,得到△ADF∽△C
1AG,△ADC
2∽△FDA,设AD=BD=a,利用勾股定理表示出AB,在Rt△ABC
1中,利用30度角的余弦函数定义表示出AC
1,用AD:AC
1即可求出△ADF与△C
1AG的相似比.
解答:解:(1)∵∠DAB=∠DBA=45°,∠CAB=30°,∠CAB=60°,∠D=∠C=90°,
∴∠DAC=∠DAB-∠CAB=45°-30°=15°,∠DBC=∠CAB-∠DBA=60°-45°=15°,
由∠AED为三角形ABE的外角,
∴∠AED=∠CEB=∠CAB+∠DBA=30°+45°=75°,
由∠DEC为三角形ADE的外角,∠AEB为三角形AED的外角,
∠DEC=∠AEB=∠DAC+∠D=90°+15°=105°,
综上,∠DAC=∠DBC=15°,∠AED=∠BEC=75°,∠CED=∠AEB=105°;
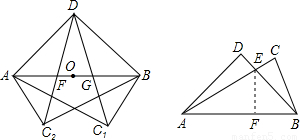
(2)过E作EF⊥AB于F点,
令AD=BD=a,EF=x,
则AB=
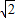
a,BF=EF=x,AF=
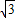
x
∴(
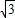
+1)x=
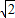
a,
解得:x=
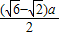
,
那么AE=2x=(
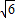
-

)a,
DE=a-

x=(2-
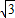
)a,
∴sin15°=
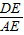
=
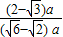
=
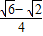
.
(3)由”直角三角形斜边上中线等于斜边的一半”可知,
点A,D,B,C
1,C
2都在以AB为直径的圆上,
则∠ADC
2=∠ABC
2=∠BAC
1=30°,∠DAB=∠DBA=∠CC
1A=45°,
∴△ADF∽△C
1AG.△ADC
2∽△FDA.
令AD=BD=a,则AB=
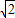
a,
在Rt△ABC
1中,AC
1=ABcos30°=
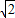
a•
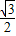
=
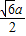
由△ADF∽△C
1AG得相似比AD:C
1A=2:
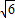
.
点评:此题考查了相似三角形的判定与性质,圆周角定理,直角三角形的性质,以及锐角三角函数的定义.要求学生借助图形,利用数形结合的数学思想,构造直角三角形,灵活运用勾股定理及锐角三角函数定义来解决数学问题.



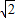 a,BF=EF=x,AF=
a,BF=EF=x,AF=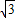 x
x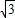 +1)x=
+1)x=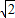 a,
a,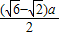 ,
,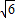 -
- )a,
)a, x=(2-
x=(2-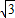 )a,
)a,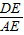 =
=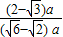 =
=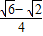 .
.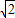 a,
a,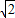 a•
a•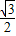 =
=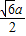
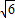 .
.

 初中学业考试导与练系列答案
初中学业考试导与练系列答案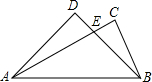 (创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,
(创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,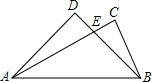 (创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,
(创新题).我们使用的三角板中有30°,45°,60°和90°特殊角,我们规定:由一副三角板中的角加,减所得的角称之为”半特殊角”.如135°=90°+45°等.如图是由两块斜边等长的三角板拚凑而成的,