
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点. 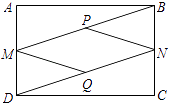
(1)求证:△MBA≌△NDC;
(2)求证:四边形MPNQ是菱形.
【答案】
(1)证明:∵四边形ABCD是矩形,
∴AB=CD,AD=BC,∠A=∠C=90°,
∵在矩形ABCD中,M、N分别是AD、BC的中点,
∴AM= ![]() AD,CN=
AD,CN= ![]() BC,
BC,
∴AM=CN,
在△MAB和△NDC中,
∵ 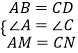 ,
,
∴△MBA≌△NDC(SAS)
(2)证明:四边形MPNQ是菱形.
理由如下:连接AP,MN,
则四边形ABNM是矩形,
∵AN和BM互相平分,
则A,P,N在同一条直线上,
易证:△ABN≌△BAM,
∴AN=BM,
∵△MAB≌△NDC,
∴BM=DN,
∵P、Q分别是BM、DN的中点,
∴PM=NQ,
∵ 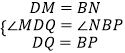 ,
,
∴△MQD≌△NPB(SAS).
∴四边形MPNQ是平行四边形,
∵M是AD中点,Q是DN中点,
∴MQ= ![]() AN,
AN,
∴MQ= ![]() BM,
BM,
∵MP= ![]() BM,
BM,
∴MP=MQ,
∴平行四边形MQNP是菱形.
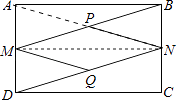
【解析】(1)根据矩形的性质和中点的定义,利用SAS判定△MBA≌△NDC;(2)四边形MPNQ是菱形,连接AN,有(1)可得到BM=DN,再有中点得到PM=NQ,再通过证明△MQD≌△NPB得到MQ=PN,从而证明四边形MPNQ是平行四边形,利用三角形中位线的性质可得:MP=MQ,进而证明四边形MQNP是菱形
【考点精析】认真审题,首先需要了解菱形的判定方法(任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形),还要掌握矩形的性质(矩形的四个角都是直角,矩形的对角线相等)的相关知识才是答题的关键.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】综合题
(1)如图①, ![]() 的内角
的内角 ![]() 的平分线与外角
的平分线与外角 ![]() 的平分线相交于
的平分线相交于 ![]() 点,
点, ![]() ,求
,求 ![]() 的度数.
的度数.
(2)如图,四边形 ![]() 中,设
中,设 ![]() ,
, ![]() ,
, ![]() 为四边形
为四边形 ![]() 的内角
的内角 ![]() 与外角
与外角 ![]() 的平分线所在直线相交而形成的锐角.
的平分线所在直线相交而形成的锐角.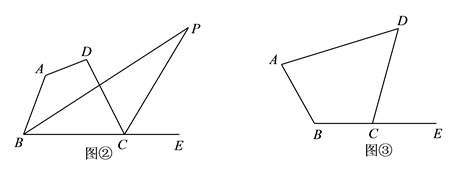
①如图②,若 ![]() ,求
,求 ![]() 的度数.(用
的度数.(用 ![]() 、
、 ![]() 的代数式表示)
的代数式表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将两块直角三角尺的直角顶点C叠放在一起.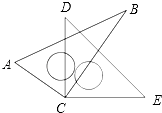
(1)写出以C为顶点的相等的锐角,并说明理由;
(2)若射线CB平分∠DCE,求∠ACE的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商家预测一种应季衬衫能畅销市场,就用13200元购进了一批这种衬衫,面市后果然供不应求,商家又用28800元购进了第二批这种衬衫,所购数量是第一批购进量的2倍,但单价贵了10元.
(1)该商家购进的第一批衬衫是多少件?
(2)若两批衬衫按相同的标价销售,最后剩下50件按八折优惠卖出,如果两批衬衫全部售完后利润不低于25%(不考虑其他因素),那么每件衬衫的标价至少是多少元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角; ③过一点有且仅有一条直线与己知直线垂直; ④两点之间的距离是两点间的线段;⑤若AB=BC,则点B为线段AC的中点。其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点,下列结论:①∠OBE= ![]() ∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是 .
∠ADO;②EG=EF;③GF平分∠AGE;④EF⊥GE,其中正确的是 . 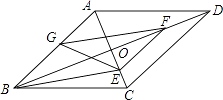
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com