
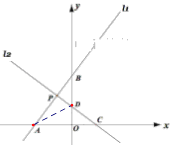
【题目】如图,直线![]() 的解析式为y=
的解析式为y=![]() x+4,与x轴y轴分别交于A,B两点;直线
x+4,与x轴y轴分别交于A,B两点;直线![]() 与x轴交于点C(2,0)与y轴交于点D(0,
与x轴交于点C(2,0)与y轴交于点D(0, ![]() ),两直线交于点P.
),两直线交于点P.
(1)求点A,B的坐标及直线![]() 的解析式;
的解析式;
(2)求证:△AOB≌△APC;
(3)若将直线![]() 向右平移m个单位,与x轴,y轴分别交于点
向右平移m个单位,与x轴,y轴分别交于点![]() 、
、![]() ,使得以点A、B、
,使得以点A、B、![]() 、
、![]() 为顶点的图形是轴对称图形,求m的值?
为顶点的图形是轴对称图形,求m的值?

【答案】(1)A(-3,0),B(0,4),l2: ![]() ;(2)证明见解析;(3)m=1.
;(2)证明见解析;(3)m=1.
【解析】试题分析:(1)根据直线![]() 的解析式为y=
的解析式为y=![]() x+4,分别令x=0、y=0即可得出A、B坐标,直线
x+4,分别令x=0、y=0即可得出A、B坐标,直线![]() 利用待定系数法即可求得;
利用待定系数法即可求得;
(2)连接AD,先证明△ADB≌△ADC,得到∠ABO=∠ACP,再根据ASA证明△AOB≌△APC即可;
(3)由B、D′都在y轴上,A、C′在x轴上,可知要想使得以点A、B、C′、D′为顶点的图形是轴对称图形,必有A、C′关于y轴对称,从而得解.
试题解析:(1)当x=0时,y=![]() x+4=4,当y=0时,0=
x+4=4,当y=0时,0=![]() x+4,解得:x=-3,
x+4,解得:x=-3,
∴A(-3,0),B(0,4),
设直线![]() 的解析式为:y=kx+b,由题意得:
的解析式为:y=kx+b,由题意得: 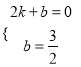 ,解得:
,解得: 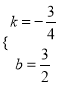 ,
,
∴直线![]() :y=
:y=![]() ;
;
(2)连接AD,
由B(0,4),D(0, ![]() ),A(-3,0),C(2,0)可得:BD=
),A(-3,0),C(2,0)可得:BD=![]() ,AC=AB=5,
,AC=AB=5,
又由OC=2,OD=![]() 得CD=
得CD=![]() =
=![]() =BD,
=BD,
在△ADB和△ADC中 ,∴△ADB≌△ADC,∴∠ABO=∠ACP,
,∴△ADB≌△ADC,∴∠ABO=∠ACP,
在△AOB和△APC中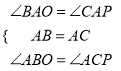 ,∴△AOB≌△APC;
,∴△AOB≌△APC;
(3)∵B、D′都在y轴上,A、C′在x轴上,
∴要想使得以点A、B、C′、D′为顶点的图形是轴对称图形,必有A、C′关于y轴对称,
∴C′(3,0),
∵C(2,0),
∴m=3-2=1.


科目:初中数学 来源: 题型:
【题目】李大爷有一块长方形菜地,且菜地的长是宽的2倍。
(1)若菜地的面积为98m2,求菜地的长与宽;
(2)若菜地的面积为90m2,这块菜地的宽是多少?(用根号表示)你能告诉李大爷这块菜地的宽在哪两个整数之间吗?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2017年《政府工作报告》中提出了十二大新词汇,为了解同学们对新词汇的关注度,某数学兴趣小组选取其中的![]() :“蓝天保卫战”,
:“蓝天保卫战”, ![]() :“数字家庭”,
:“数字家庭”, ![]() :“人工智能+第五代移动通信”,
:“人工智能+第五代移动通信”, ![]() :“全域旅游”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词、根据调查结果,该小组绘制了两幅不完整的统计图如图所示,请你根据统计图提供的信息,解答下列问题:
:“全域旅游”四个热词在全校学生中进行了抽样调查,要求被调查的每位同学只能从中选择一个我最关注的热词、根据调查结果,该小组绘制了两幅不完整的统计图如图所示,请你根据统计图提供的信息,解答下列问题:
(1)本次调查中,一共调查了多少名同学?
(2)条形统计图中, ![]() ,
, ![]() .
.
(3)若该校有![]() 名同学,请估计出选择
名同学,请估计出选择![]() 、
、![]() 的一共有多少名同学?
的一共有多少名同学?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,BC=2AB,对角线相交于O,过C点作CE⊥BD交BD于E点,H为BC中点,连接AH交BD于G点,交EC的延长线于F点,下列5个结论:①EH=AB;②∠ABG=∠HEC;③△ABG≌△HEC;④S△GAD=S四边形GHCE;⑤CF=BD.正确的有( )个.

A. 2 B. 3 C. 4 D. 5
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,AB=5,AD=3,点P是AB边上一点(不与A,B重合),连接CP,过点P作PQ⊥CP交AD边于点Q,连接CQ.
(1)当△CDQ≌△CPQ时,求AQ的长;
(2)取CQ的中点M,连接MD,MP,若MD⊥MP,求AQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形ABCD中,M、N分别是AD、BC的中点,P、Q分别是BM、DN的中点.
(1)求证:△MBA≌△NDC;
(2)四边形MPNQ是什么样的特殊四边形?请说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一次函数![]() 的图象过点
的图象过点![]() ,与函数
,与函数![]() 的图象相交于
的图象相交于![]() .
.
(1)求![]() 的值;
的值;
(2)若函数![]() 的图象与
的图象与![]() 轴的交点是B,函数
轴的交点是B,函数![]() 的图象与
的图象与![]() 轴的交点是C,与x轴交于点D,求三角形ABD的面积(其中O为坐标原点).
轴的交点是C,与x轴交于点D,求三角形ABD的面积(其中O为坐标原点).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com