
 BD2,再利用二次函数的求最值问题,即可求四边形ABCD的面积.
BD2,再利用二次函数的求最值问题,即可求四边形ABCD的面积.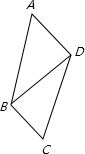 解:如右图所示,连接BD,
解:如右图所示,连接BD, AD•BDsin∠ADB,
AD•BDsin∠ADB, BD•BCsin∠BCD,
BD•BCsin∠BCD, AD•BD+
AD•BD+ BD•BC,
BD•BC, BD(16-BD)=8BD-
BD(16-BD)=8BD- BD2,
BD2, <0,
<0, =8时,四边形ABCD的面积有最大值=
=8时,四边形ABCD的面积有最大值= =32.
=32.

 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:
| A、2个 | B、3个 | C、4个 | D、6个 |
查看答案和解析>>
科目:初中数学 来源: 题型:
| 年 份 | 2001 | 2002 | 2003 | 2004 | … |
| 财政收入 单位(亿元) |
10 | 10.5 | 12 | 14.5 | … |
查看答案和解析>>
科目:初中数学 来源: 题型:
 如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,
如图,已知四边形ABCD中,E、F、G、H分别为AB、BC、CD、DA的中点,查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com