
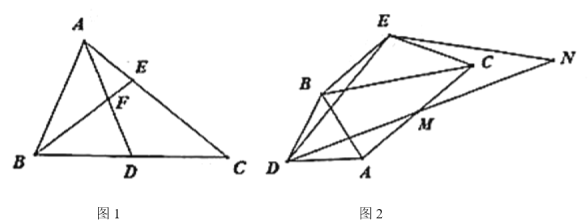
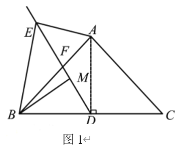
【题目】如图1,在![]() 中,
中,![]() 分别为
分别为![]() 上一点,且
上一点,且![]() ,
,![]() ,
,![]() .
.
(1)求证:![]() ;
;
(2)求证:![]() ;
;
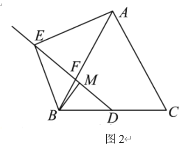
(3)若![]() ,将
,将![]() 绕
绕![]() 顺时针旋转至如图2所示位置(
顺时针旋转至如图2所示位置(![]() 不动),连
不动),连![]() ,取
,取![]() 中点
中点![]() ,连
,连![]() ,
,![]() 为射线
为射线![]() 上一点,连
上一点,连![]() ,求
,求![]() 的最小值.
的最小值.
【答案】(1)见解析;(2)见解析;(3)![]()
【解析】
(1)由![]() 可得
可得![]() ,由
,由![]() 可得
可得![]() ,可证
,可证![]()
(2)延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,在
,在![]() 上截取
上截取![]() ,连
,连![]() ,可证:
,可证:![]() 可得
可得![]() ,可证:
,可证:![]() 可得
可得![]() ,故
,故![]() 即可证
即可证![]()
(3)延长![]() 至
至![]() 使
使![]() ,连
,连![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于
交于![]() ,
,![]() 交
交![]() 于
于![]()
可证:![]() ,故
,故![]() ,
,![]() ,
,![]() ,由(2)知
,由(2)知![]() ,由于
,由于![]() 故可得
故可得![]() 故
故![]() ,故
,故![]() .故
.故![]() 可证
可证![]() ,可得
,可得![]() ,
,![]() 可证
可证![]() 为正三角形,故
为正三角形,故![]() ,由于
,由于![]() 故
故![]() 即可求出
即可求出![]() 的最小值.
的最小值.
(1)证明:![]()
又![]()
![]()
![]()
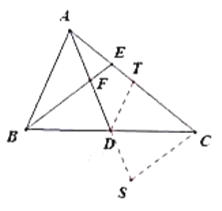
(2)证明:延长![]() 至
至![]() ,使
,使![]() ,连
,连![]() ,在
,在![]() 上截取
上截取![]() ,连
,连![]() .
.
∵BD=CD,∠BDF=∠CDS
∴![]()
∵∠TCD =∠EBC
∴∠TCD=∠DCS
∵TC=SC,CD=CD
∴![]()
![]()
![]() .
.
∴![]()
(3)解:延长![]() 至
至![]() 使
使![]() ,
,
连![]() ,
,![]() ,延长
,延长![]() ,
,![]() 交于
交于![]() ,
,![]() 交
交![]() 于
于![]()
∵M是AC的中点
∴AM=MC
∵∠CME=∠SMA,EM=MS
∴![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
由(2)知![]()
![]()
![]()
![]() .
.
![]()
在![]() 和
和![]() 中
中
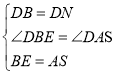
![]()
![]()
![]()
![]() 为正三角形,
为正三角形,![]()
![]()
![]() 的最小值为
的最小值为![]()


科目:初中数学 来源: 题型:
【题目】已知:如图,在平行四边形ABCD中,E、F分别为边AB、CD的中点,BD是对角线,AG∥DB交CB的延长线于G.

(1)求证:△ADE≌△CBF;
(2)若四边形 BEDF是菱形,则四边形AGBD是什么特殊四边形?并证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一个不透明的盒子里装有5个分别写有数字0,1,2,3,4的小球,它们除数字不同外其余全部相同.现从盒子里随机摸出一个小球(不放回),设该小球上的数字为m,再从盒子中摸出一个小球,设该小球上的数字为n,点P的坐标为![]() ,则点P落在抛物线
,则点P落在抛物线![]() 与x轴所围成的区域内(含边界)的概率是________.
与x轴所围成的区域内(含边界)的概率是________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在矩形![]() 中,
中,![]() ,对角线
,对角线![]() ,
,![]() 相交于点
相交于点![]() ,动点
,动点![]() 由点
由点![]() 出发,沿
出发,沿![]() 向点
向点![]() 运动.设点
运动.设点![]() 的运动路程为
的运动路程为![]() ,
,![]() 的面积为
的面积为![]() ,
,![]() 与
与![]() 的函数关系图象如图②所示,则
的函数关系图象如图②所示,则![]() 边的长为__________.
边的长为__________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:在![]() 中,
中,![]() ,点
,点![]() 为
为![]() 边的中点,点
边的中点,点![]() 在
在![]() 上,连接
上,连接![]() 并延长到点
并延长到点![]() ,使
,使![]() ,点
,点![]() 在线段
在线段![]() 上,且
上,且![]() .
.
(1)如图1,连接![]() ,当
,当![]() 时,求证:
时,求证:![]()
(2)如图2,当![]() 时,则线段
时,则线段![]() 之间的数量关系为 ;
之间的数量关系为 ;

(3)在(2)的条件下,延长![]() 到
到![]() ,使
,使![]() ,连接
,连接![]() ,若
,若![]() ,
,![]() ,求证:
,求证:![]() ,并求
,并求![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】关注数学文化:古希腊的几何学家海伦在数学史上以解决几何测量问题而闻名.在他的著作《度量》一书中,给出了如下公式:若一个三角形的三边长分别为a,b,c,记p=![]() ,则三角形的面积S=
,则三角形的面积S=![]() (海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式:
(海伦公式).我国南宋时期数学家秦九韶曾提出利用三角形的三边求面积的秦九韶公式: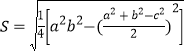 .海伦公式和秦九韶公式实质上是同一个公式,所以我们一般也称此公式为海伦-秦九韶公式.
.海伦公式和秦九韶公式实质上是同一个公式,所以我们一般也称此公式为海伦-秦九韶公式.
若△ABC的三边长分别为5,6,7,△DEF的三边长分别为![]() ,
,![]() ,
,![]() ,请选择合适的公式分别求出△ABC和△DEF的面积.
,请选择合适的公式分别求出△ABC和△DEF的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一袋中装有形状大小都相同的四个小球,每个小球上各标有一个数字,分别是1,4,7,8.现规定从袋中任取一个小球,对应的数字作为一个两位数的个位数;然后将小球放回袋中并搅拌均匀,再任取一个小球,对应的数字作为这个两位数的十位数.
(1)写出按上述规定得到所有可能的两位数;
(2)从这些两位数中任取一个,求其算术平方根大于4且小于7的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对钝角α,定义三角函数值如下:
sinα=sin(180°-α),cosα=-cos(180°-α).
(1)求sin120°,cos120°的值;
(2)若一个钝角三角形的三个内角比是1:1:4,点A,B是这个三角形的两个顶点,sinA,cosB是方程4x2-mx-1=0的两个不相等的实数根,求m的值及∠A和∠B的度数.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com