
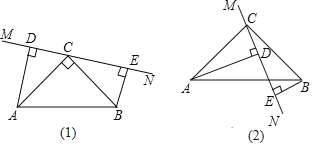
【题目】在△ABC中,∠ACB=90![]() ,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)当直线MN如图(1)的位置时,
求证:①△ADC≌△CEB ②DE=AD+BE
(2)当直线MN绕点C旋转到图(2)的位置时,直接写出DE、AD、BE三者之间的关系 .
【答案】(1)①证明见解析;②证明见解析;(2)DE=AD-BE,理由见解析.
【解析】
(1)①由∠ACB=90°,得∠ACD+∠BCE=90°,而AD⊥MN于D,BE⊥MN于E,则∠ADC=∠CEB=90°,根据等角的余角相等得到∠ACD=∠CBE,根据AAS即可证得Rt△ADC≌Rt△CEB;
②由①中的全等可得AD=CE,DC=BE,根据线段的和差即可求得结论;
(2)根据等角的余角相等得到∠ACD=∠CBE,易得△ADC≌△CEB,得到AD=CE,DC=BE,继而可得DE、AD、BE间的关系.
(1)①∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
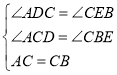 ,
,
∴△ADC≌△CEB;
②∵△ADC≌△CEB,
∴AD=CE,DC=BE,
∵DE=DC+CE,
∴DE=AD+BE;
(2)DE=AD-BE,理由如下:
∵∠ACB=90°,
∴∠ACD+∠BCE=90°,
又∵AD⊥MN,BE⊥MN,
∴∠ADC=∠CEB=90°,∠BCE+∠CBE=90°,
∴∠ACD=∠CBE,
在△ADC和△CEB中,
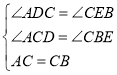 ,
,
∴△ADC≌△CEB;
∴AD=CE,DC=BE,
∵DE=CE-CD,
∴DE=AD-BE.


 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案 南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,∠A=90°,E在AD上,且CE平分∠BCD,BE平分∠ABC,则下列关系式中成立的有( )
①![]() ; ②
; ②![]() ;③
;③![]() ;④
;④![]() ; ⑤
; ⑤![]()

A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】仙降是瑞安重要的制鞋基地,其生产的鞋子畅销世界各地,某制鞋企业欲将![]() 件产品运往
件产品运往![]() 三地销售,运往
三地销售,运往![]() 地的费用为18元/件,运往
地的费用为18元/件,运往![]() 地的费用为20元/件,运往
地的费用为20元/件,运往![]() 地的费用为17元/件,要求运往
地的费用为17元/件,要求运往![]() 地的件数与运往
地的件数与运往![]() 地的件数相同. 设安排
地的件数相同. 设安排![]() 件产品运往
件产品运往![]() 地.
地.
(1)若![]() ①运往
①运往![]() 地件数为 件(用含
地件数为 件(用含![]() 的代数式表示);②若总运费不超过1850元,则运往
的代数式表示);②若总运费不超过1850元,则运往![]() 地至少有多少件?
地至少有多少件?
(2)若总运费为1900元,则![]() 的最大值为 .(直接写出答案)
的最大值为 .(直接写出答案)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一个分式的分子或分母可以因式分解,且这个分式不可约分,那么我们称这个分式为“和谐分式”
(1)下列分式中, 是和谐分式(填序号即可)
①![]() ②
②![]() ③
③![]() ④
④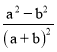
(2)若![]() 为正整数,且
为正整数,且![]() 为和谐分式,请写出所有
为和谐分式,请写出所有![]() 的值
的值
(3)在化简![]() 时,
时,
小强进行了如下三步变形:
原式=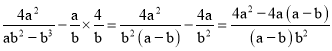
请你接着小强的方法完成化简.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平行四边形ABCD中,按以下步骤作图:①以A为圆心,任意长为半径作弧,分别交AB,AD于点M,N;②分别以M,N为圆心,以大于![]() MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.
MN的长为半径作弧,两弧相交于点P;③作AP射线,交边CD于点Q,若DQ=2QC,BC=3,则平行四边形ABCD周长为________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】若二次函数y=x2+![]() 与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
与y=-x2+k的图象的顶点重合,则下列结论不正确的是( )
A. 这两个函数图象有相同的对称轴 B. 这两个函数图象的开口方向相反
C. 方程-x2+k=0没有实数根 D. 二次函数y=-x2+k的最大值为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,![]() 的顶点坐标分别为
的顶点坐标分别为![]() ,
,![]() ,
,![]() ,把
,把![]() 沿直线
沿直线![]() 翻折,点
翻折,点![]() 的对应点为
的对应点为![]() ,抛物线
,抛物线![]() 经过点
经过点![]() ,顶点
,顶点![]() 在直线
在直线![]() 上.
上.

![]() 证明四边形
证明四边形![]() 是菱形,并求点
是菱形,并求点![]() 的坐标;
的坐标;
![]() 求抛物线的对称轴和函数表达式;
求抛物线的对称轴和函数表达式;
![]() 在抛物线上是否存在点
在抛物线上是否存在点![]() ,使得
,使得![]() 与
与![]() 的面积相等?若存在,直接写出点
的面积相等?若存在,直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com