
【题目】已知二次函数![]() .
.
(1)在给定的直角坐标系中,画出这个函数的图象;
(2)根据图象,写出当![]() 时,
时,![]() 的取值范围;
的取值范围;
(3)若将此图象沿![]() 轴向左平移3个单位,向下移动2个单位,请写出平移后图象所对应的函数表达式.
轴向左平移3个单位,向下移动2个单位,请写出平移后图象所对应的函数表达式.
 海淀黄冈名师导航系列答案
海淀黄冈名师导航系列答案 普通高中同步练习册系列答案
普通高中同步练习册系列答案科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线![]() 与
与![]() 轴交于点
轴交于点![]() 和
和![]() ,与
,与![]() 轴交于点
轴交于点![]() .
.
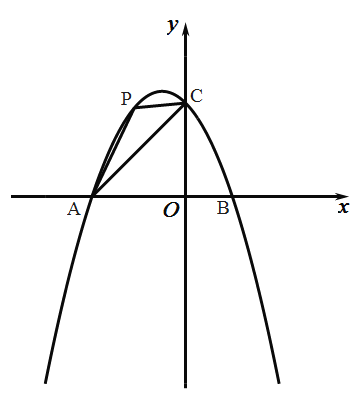
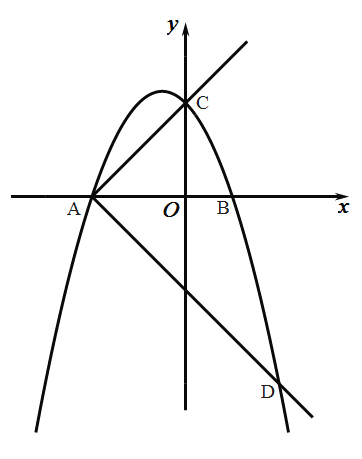
(1)求抛物线的表达式;
(2)点![]() 是抛物线上第二象限内的点,连接
是抛物线上第二象限内的点,连接![]() ,设
,设![]() 的面积为
的面积为![]() ,当
,当![]() 取最大值时,求点
取最大值时,求点![]() 的坐标;
的坐标;
(3)作射线![]() ,将射线
,将射线![]() 绕
绕![]() 点顺时针旋转
点顺时针旋转![]() 交抛物线于另一点
交抛物线于另一点![]() ,在射线
,在射线![]() 上是否存在一点
上是否存在一点![]() ,使
,使![]() 的周长最小.若存在,求出
的周长最小.若存在,求出![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
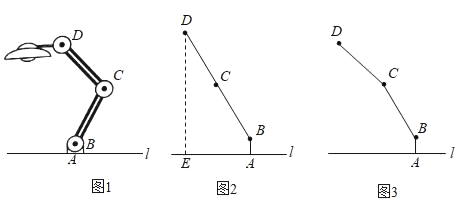
【题目】如图1为放置在水平桌面l上的台灯,底座的高AB为5cm,长度均为20cm的连杆BC、CD与AB始终在同一平面上.
(1)转动连杆BC,CD,使∠BCD成平角,∠ABC=150°,如图2,求连杆端点D离桌面l的高度DE.
(2)将(1)中的连杆CD再绕点C逆时针旋转,经试验后发现,如图3,当∠BCD=150°时台灯光线最佳.求此时连杆端点D离桌面l的高度比原来降低了多少厘米?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图为住宅区内的两幢楼,它们的高AB=CD=30m,两楼之间的距离AC=24m,现需了解甲楼对乙楼的采光的影响情况,当太阳光与水平线的夹角为30°时,求甲楼的影子在乙楼上有多高?(精确到0.1m,![]() ≈1.41,
≈1.41,![]() ≈1.73)?
≈1.73)?

查看答案和解析>>
科目:初中数学 来源: 题型:
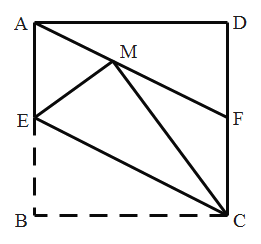
【题目】如图,在正方形![]() 中,
中,![]() 是
是![]() 边的中点,将
边的中点,将![]() 沿
沿![]() 折叠,使点
折叠,使点![]() 落在点
落在点![]() 处,
处,![]() 的延长线与
的延长线与![]() 边交于点
边交于点![]() .下列四个结论:①
.下列四个结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() S正方形ABCD,其中正确结论的个数为( )
S正方形ABCD,其中正确结论的个数为( )
A.![]() 个B.
个B.![]() 个C.
个C.![]() 个D.
个D.![]() 个
个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等边![]() 的边长为
的边长为![]() ,等边
,等边![]() 的边长为
的边长为![]() ,把
,把![]() 放在
放在![]() 中,使
中,使![]() 与
与![]() 重合,点
重合,点![]() 在
在![]() 边上,如图所示,此时点
边上,如图所示,此时点![]() 是
是![]() 中点,在
中点,在![]() 内部将
内部将![]() 按下列方式旋转:绕点
按下列方式旋转:绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,完成第
重合,完成第![]() 次操作,此时点
次操作,此时点![]() 是
是![]() 中点,
中点,![]() 旋转了__________
旋转了__________![]() ;再绕点
;再绕点![]() 顺时针旋转,使点
顺时针旋转,使点![]() 与点
与点![]() 重合,完成第
重合,完成第![]() 次操作;……这样依次绕
次操作;……这样依次绕![]() 的某个顶点连续旋转下去,第
的某个顶点连续旋转下去,第![]() 次操作完成时,
次操作完成时,![]() _____________.
_____________.
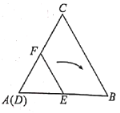
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,已知某个二次函数的图象经过点A(1,2),B(2,﹣1),C(4,﹣1),且该二次函数的最小值是﹣2.

(1)请在图中描出该函数图象上另外的两个点,并画出图象;
(2)求出该二次函数的解析.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】定义:我们知道,四边形的一条对角线把这个四边形分成了两个三角形,如果这两个三角形相似(不全等),我们就把这条对角线叫做这个四边形的“相似对角线”.
理解:(1)如图1,已知Rt△ABC在正方形网格中,请你只用无刻度的直尺在网格中找到一点D,使四边形ABCD是以AC为“相似对角线”的四边形(保留画图痕迹,找出3个即可);
(2)如图2,在四边形ABCD中,∠ABC=80°,∠ADC=140°,对角线BD平分∠ABC.求证:BD是四边形ABCD的“相似对角线”.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com