
����Ŀ�����ż�¼Ƭ��֮�¡��IJ�����ȫ���Կ�����Ⱦ����Խ��Խ���ӣ�����������������Ҳ������ij�̳��ӳ��ҹ�����A��B�����ͺŵĿ�������������֪һ̨A�Ϳ����������Ľ��۱�һ̨B�Ϳ����������Ľ��۶�300Ԫ����7 500Ԫ����A�Ϳ�������������6 000Ԫ����B�Ϳ�����������̨����ͬ��
��1����һ̨A�Ϳ�����������һ̨B�Ϳ����������Ľ��۸�Ϊ����Ԫ��
��2�����г����飬��B�Ϳ������������ۼ�Ϊ1800Ԫʱ��ÿ�������4̨���ڴ˻����ϣ��ۼ�ÿ����50Ԫ��ÿ�콫���۳�1̨�����ÿ���̳�����B�Ϳ���������������Ϊ3200Ԫ�����ʸ��̳�Ӧ��B�Ϳ������������ۼ۶�Ϊ����Ԫ��
��3����֪A�Ϳ�����������������Ϊ340m3/h��B�Ϳ�����������������Ϊ240m3/h��ij��˾���ڰ칫���������Ϊ600m2������ǽ��3.5m���ܶ�̥����Ӱ�죬�����и�����������Ϊ��֤̥�������ɳ����ù�˾�ƻ�����15̨��������������������ÿ�컨��30���ӽ����ڿ�������һ�£��������ǿ������������أ��ù�˾����Ҫ����A�Ϳ�������������̨��
���𰸡���1��һ̨A�Ϳ�����������һ̨B�Ϳ����������Ľ��۷ֱ�Ϊ1500Ԫ��1200Ԫ��
��2�����̳�Ӧ��B�Ϳ������������ۼ۶�Ϊ1600Ԫ��
��3���ù�˾����Ҫ����A�Ϳ���������6̨��
��������
�����������1����һ̨B�Ϳ����������Ľ���ΪxԪ����һ̨A�Ϳ����������Ľ���Ϊ��x+300��Ԫ��������7 500Ԫ����A�Ϳ�������������6 000Ԫ����B�Ϳ�����������̨����ͬ���з���![]() =
=![]() ��Ȼ��ⷽ�̼���ȷ��x��ֵ���ټ���x+300���ɣ�
��Ȼ��ⷽ�̼���ȷ��x��ֵ���ټ���x+300���ɣ�
��2������̳�Ӧ��B�Ϳ������������ۼ۶�ΪaԪ����������Ϊ��4+![]() ��̨��Ȼ�����õ�����������������з��̣�a��1200����4+
��̨��Ȼ�����õ�����������������з��̣�a��1200����4+![]() ��=3200���ٽ�һԪ���η��̼��ɣ�
��=3200���ٽ�һԪ���η��̼��ɣ�
��3���ù�˾Ҫ����A�Ϳ���������m̨�����þ�������������ڰ칫�ҵ�����в���ʽ![]() [340m+240��15��m��]��600��3.5��Ȼ��ⷽ�̵õ�m�ķ�Χ���ڴ˷�Χ��ȷ��m����Сֵ���ɣ�
[340m+240��15��m��]��600��3.5��Ȼ��ⷽ�̵õ�m�ķ�Χ���ڴ˷�Χ��ȷ��m����Сֵ���ɣ�
�����������1����һ̨B�Ϳ����������Ľ���ΪxԪ����һ̨A�Ϳ����������Ľ���Ϊ��x+300��Ԫ��
���������![]() =
=![]() ��
��
���x=1200��
������x=1200��ԭ���̵Ľ⣬
��x=1200ʱ��x+300=1500��
����һ̨A�Ϳ�����������һ̨B�Ϳ����������Ľ��۷ֱ�Ϊ1500Ԫ��1200Ԫ��
��2������̳�Ӧ��B�Ϳ������������ۼ۶�ΪaԪ��
��������ã�a��1200����4+![]() ��=3200��
��=3200��
������a2��3200a+2560000=0�����a1=a2=160��
���Ը��̳�Ӧ��B�Ϳ������������ۼ۶�Ϊ1600Ԫ��
��3���ù�˾Ҫ����A�Ϳ���������m̨��
���������![]() [340m+240��15��m��]��600��3.5
[340m+240��15��m��]��600��3.5
���m��6��
���Ըù�˾����Ҫ����A�Ϳ���������6̨��



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
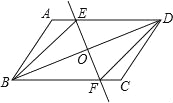
����Ŀ����֪����ͼ����ABCD�У�OΪ�Խ���BD���е㣬����O��ֱ��EF�ֱ�AD��BC��E��F���㣬����BE��DF��
��1����֤����DOE�ա�BOF��
��2������DOE���ڶ��ٶ�ʱ���ı���BFDEΪ���Σ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AE=CF����AFD=��CEB����ô��������һ�������������ж���ADF�ա�CBE���ǣ� ��
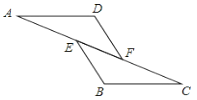
A. ��A=��C B. AD=CB C. BE=DF D. AD��BC
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��һֻ�����ڵ�һ����x�ᡢy�����������ڵ�һ���ӣ�����ԭ��������(0��1)��Ȼ����Ű�ͼ�м�ͷ��ʾ������������(0��0)��(0��1�� ��(1��1)����1��0����������ÿ������һ����λ����ô��35��ʱ��������λ�õ������ǣ� �� 
A.(4��0)
B.(5��0)
C.(0��5)
D.(5��5)
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��![]() ��
�� ![]() ��ƽ��ֱ������ϵ�е�λ����ͼ.
��ƽ��ֱ������ϵ�е�λ����ͼ.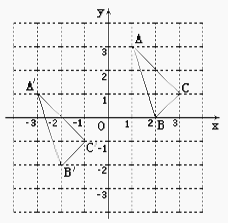
��1���ֱ�д�����и�������꣺![]() ��
�� ![]() ��
�� ![]() ��
��
��2��˵�� ![]() ��
�� ![]() ����������ƽ�Ƶõ�:��
����������ƽ�Ƶõ�:��
��3������ ![]() ��
�� ![]() ��
�� ![]() ����
���� ![]() �ڲ�һ�㣬��ƽ�ƺ�
�ڲ�һ�㣬��ƽ�ƺ� ![]() �ڵĶ�Ӧ��
�ڵĶ�Ӧ�� ![]() ������Ϊ��
��������
��4���� ![]() �����.
�����.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
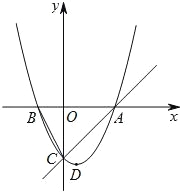
����Ŀ����ͼ����֪������y=ax2+bx+c�Ķ���D������Ϊ��1����![]() ��������x�ύ��A��B���㣬��y�ύ��C�㣬A�������Ϊ��4��0����P�����������ϵ�һ�����㣬�Һ�����Ϊm��
��������x�ύ��A��B���㣬��y�ύ��C�㣬A�������Ϊ��4��0����P�����������ϵ�һ�����㣬�Һ�����Ϊm��
��1��������������Ӧ�Ķ��κ����ı���ʽ��
��2��������P������PAO������45�㣬��P��ĺ�����m��ȡֵ��Χ��
��3���Ƿ����P�㣬ʹ��PAC=��BCO�������ڣ���ֱ��д����P�����ꣻ�������ڣ���˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����֪AD��CB����1����2����BAE����DCF����˵����
��1��AE��CF��
��2��AB��CD��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ���ڵ���ֱ��������ABC������BAC��90�㣬P����ABC��һ����PA��1��PB��3��PC��![]() .����CPA�Ķ�����
.����CPA�Ķ�����

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com