练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】[阅读]

    在平面直角坐标系中，以任意两点P（ x1，y1）、Q（x2，y2）为端点的线段中点坐标为（，）．

    [运用]

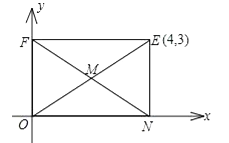
    （1）如图，矩形ONEF的对角线相交于点M，ON、OF分别在x轴和y轴上，O为坐标原点，点E的坐标为（4，3），则点M的坐标为 ．

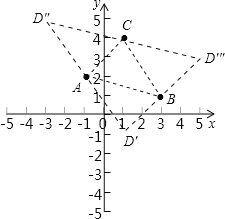
    （2）在直角坐标系中，有A（﹣1，2），B（3，1），C（1，4）三点，另有一点D与点A、B、C构成平行四边形的顶点，求点D的坐标．

    【答案】M（2，1.5）；（2）D（1，﹣1）或D（﹣3，5）或D（5，3）．

    【解析】试题分析：(1)先根据四边形ONEF是矩形,所以矩形的性质可以知道点M是对角线OE的中点,根据题中给出的线段的中点坐标公式即可得出M点的坐标;
    (2)根据题意画出图形,然后分三种情况：①当AB为对角线时, ②当BC为对角线时, ③当AC为对角线时，求出点D的坐标.

    解:(1)四边形ONEF是矩形,且,

    点M是对角线OE的中点,

    ,即.

    因此，本题正确答案是:;

    (2)如图所示:

    根据平行四边形的对角线互相平分可得:

    设D点的坐标为,

    以点A、B、C、D构成的四边形是平行四边形,

    ①当AB为对角线时,

    ,,,

    ,

    ,
    ,,

    点坐标为,

    ②当BC为对角线时,

    ,,,

    ,,

    D点坐标为.

    ③当AC为对角线时,

    ,,,

    ,,

    D点坐标为:,

    综上所述,符合要求的点有:,,.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】问题探究：
    （1）如图①，点M、N分别为四边形ABCD边AD、BC的中点，则四边形BNDM的面积与四边形ABCD的面积关系是 ．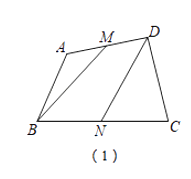

    （2）如图②，在四边形ABCD中，点M、N分别为AD、BC的中点，MB交AN于点P，MC交DN于点Q，若S△四边形MPNQ=10，则S△ABP+S△DCQ的值为多少？
    （3）问题解决
    在矩形ABCD中，AD=2，DC=4，点M、N为AB上两点，且满足BN=2AM=2MN，连接MC、MD．若点P为CD上任意一点，连接AP、NP，使得AP与DM交于点E，NP与MC交于点F，则四边形MEPF的面积是否存最大值？若存在，请求出最大面积；若不存在，请说明理由．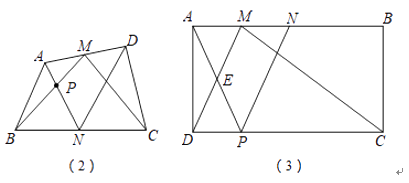

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在△ABC中，D、E分别是AB、AC的中点，过点E作EF∥AB，交BC于点F．

    （1）求证：四边形DBFE是平行四边形；

    （2）当△ABC满足什么条件时，四边形DBEF是菱形？为什么？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在平面直角坐标系中，点A(t+1,t+2),点B(t+3,t+1),将点A向右平移3个长度单位，再向下平移4个长度单位得到点C.

    （1）用t表示点C的坐标为_______;用t表示点B到y轴的距离为___________;

    （2）若t=1时，平移线段AB，使点A、B到坐标轴上的点、处，指出平移的方向和距离，并求出点、的坐标；

    （3）若t=0时，平移线段AB至MN（点A与点M对应），使点Ｍ落在ｘ轴的负半轴上，三角形MNB的面积为4，试求点M、N的坐标.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在△ABC和△DEF中，将△DEF按要求摆放，使得∠D的两条边分别经过点B和点C．

    （1）当将△DEF如图1摆放时，若∠A=50°，∠E+∠F=100°，则∠D= ；∠ABD+∠ACD＝ ．

    （2）当将△DEF如图2摆放时，∠A=m°，∠E+∠F=n°，请求出∠ABD+∠ACD的度数(用含m、n的代数式表示)．

    （3）能否将△DEF摆放到某个位置，使得BD、CD同时平分∠ABC和∠ACB．若能，求出∠A、∠E、∠F满足的关系？若不能，请说明理由？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】小明骑单车上学，当他骑了一段路时，想起要买某本书，于是又折回到刚经过的某书店，买到书后继续去学校．以下是他本次上学所用的时间与路程的关系示意图．根据图中提供的信息回答下列问题：

    （1）小明家到学校的路程是 米．

    （2）小明在书店停留了 分钟．

    （3）本次上学途中，小明一共行驶了 米．一共用了 分钟．

    （4）我们认为骑单车的速度超过 300 米/分就超过了安全限度．问：在整个上学途中哪个时间段小明的骑车速度最快，最快速度为多少，在安全限度内吗？

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，直角坐标系中，的顶点都在网格点上，其中，点坐标为，

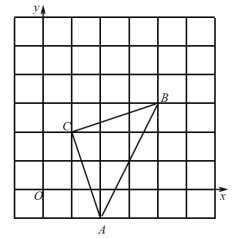
    （1）写出点、的坐标：（____，____）、（____，____）

    （2）将先向左平移个单位长度，再向上平移个单位长度，得到，画出；

    （3）写出三个顶点坐标（___，___）、（___，___）、（___，___）；

    （4）求的面积．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图1，已知，是等边三角形，点为射线上任意一点（点与点不重合），连结，将线段绕点逆时针旋转得到线段，连结并延长交射线于点．

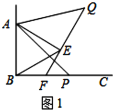
    （1）如图1，当时，________，猜想________；

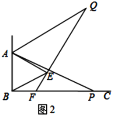
    （2）如图2，当点为射线上任意一点时，猜想的度数，并说明理由；

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】一次函数y=ax+b和反比例函数y= 在同一平面直角坐标系中的图象如图所示，则二次函数y=ax2+bx+c的图象大致为（ ）

    A.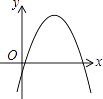
    B.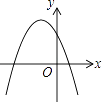
    C.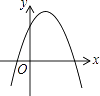
    D.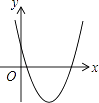

    查看答案和解析>>

    同步练习册答案