
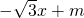 (m为实数)的图象为直线l,l分别交x,y于A,B两点,以坐标原点O为
(m为实数)的图象为直线l,l分别交x,y于A,B两点,以坐标原点O为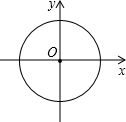 圆心的圆的半径为1.
圆心的圆的半径为1. m
m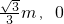 ),B点坐标为(0,m).
),B点坐标为(0,m).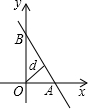 OA=
OA= |m|,OB=|m|,
|m|,OB=|m|, =
= ,∴∠BAO=60°
,∴∠BAO=60°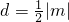 ,
, =1,
=1,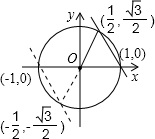 O与x轴的交点(1,0)或(-1,0)
O与x轴的交点(1,0)或(-1,0) x+m中,
x+m中,
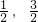 )或(
)或(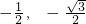 )
)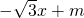 ,令y=0求得A点坐标,x=0时求得B点坐标;
,令y=0求得A点坐标,x=0时求得B点坐标;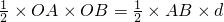 ”得出d的值,当d=1时,直线1与⊙O相切;
”得出d的值,当d=1时,直线1与⊙O相切;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
 如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )
如图所示,已知一次函数y1=kx+b的图象经过A(1,2)、B(-1,0)两点,y2=mx+n的图象经过A、C(3,0)两点,则不等式组0<kx+b<mx+n的解集是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com