
 是什么类型的弧时,△CED的外心在△CED的外部、内部、一边上.(只写结论,不用证明)
是什么类型的弧时,△CED的外心在△CED的外部、内部、一边上.(只写结论,不用证明)
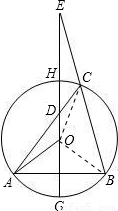 (1)证明:连接OB,
(1)证明:连接OB,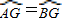 .
. ∠AOB.
∠AOB. ∠AOB,
∠AOB, =
=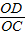 .
. 是劣弧时,△CED的外心在△CED的外部;
是劣弧时,△CED的外心在△CED的外部; 是半圆时,△CED的外心在△CED的边上;
是半圆时,△CED的外心在△CED的边上; 是优弧时,△CED的外心在△CED的内部.
是优弧时,△CED的外心在△CED的内部.

科目:初中数学 来源:2006年全国中考数学试题汇编《一次函数》(08)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年广西贺州市中考数学试卷(大纲卷)(解析版) 题型:解答题
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《平面直角坐标系》(02)(解析版) 题型:填空题
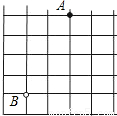
查看答案和解析>>
科目:初中数学 来源:2006年广西贺州市中考数学试卷(大纲卷)(解析版) 题型:选择题
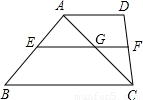
查看答案和解析>>
科目:初中数学 来源:2006年广西贺州市中考数学试卷(大纲卷)(解析版) 题型:选择题
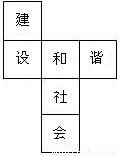 (2006•贺州)如图是一个正方体的展开图,将它折叠成正方体后,“建”字的对面是( )
(2006•贺州)如图是一个正方体的展开图,将它折叠成正方体后,“建”字的对面是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com