
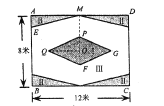
ЁОЬтФПЁПШчЭМЃЌФГаЃзМБИИјГЄ12УзЃЌПэ8УзЕФОиаЮ![]() ЪвФкГЁЕиНјааЕиУцзАЪЮЃЌЯжНЋЦфЛЎЗжЮЊЧјгђЂёЃЈСтаЮ
ЪвФкГЁЕиНјааЕиУцзАЪЮЃЌЯжНЋЦфЛЎЗжЮЊЧјгђЂёЃЈСтаЮ![]() ЃЉЃЌЧјгђЂђЃЈ4ИіШЋЕШЕФжБНЧШ§НЧаЮЃЉЃЌЪЃгрПеАзВПЗжМЧЮЊЧјгђЂѓЃЛЕу
ЃЉЃЌЧјгђЂђЃЈ4ИіШЋЕШЕФжБНЧШ§НЧаЮЃЉЃЌЪЃгрПеАзВПЗжМЧЮЊЧјгђЂѓЃЛЕу![]() ЮЊОиаЮКЭСтаЮЕФЖдГЦжааФЃЌ
ЮЊОиаЮКЭСтаЮЕФЖдГЦжааФЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЮЊСЫУРЙлЃЌвЊЧѓЧјгђЂђЕФУцЛ§ВЛГЌЙ§ОиаЮ
ЃЌЮЊСЫУРЙлЃЌвЊЧѓЧјгђЂђЕФУцЛ§ВЛГЌЙ§ОиаЮ![]() УцЛ§ЕФ
УцЛ§ЕФ![]() ЃЌШєЩш
ЃЌШєЩш![]() Уз.
Уз.
Мз | вв | Бћ | |
ЕЅМлЃЈдЊ/Уз2ЃЉ |
|
|
|
ЃЈ1ЃЉЕБ![]() ЪБЃЌЧѓЧјгђЂђЕФУцЛ§.
ЪБЃЌЧѓЧјгђЂђЕФУцЛ§.
ЃЈ2ЃЉМЦЛЎдкЧјгђЂёЃЌЂђЗжБ№ЦЬЩшМзЃЌввСНПюВЛЭЌЕФЩюЩЋДЩзЉЃЌЧјгђЂѓЦЬЩшБћПюАзЩЋДЩзЉЃЌ
ЂйдкЯрЭЌЙтееЬѕМўЯТЃЌЕБГЁЕиФкАзЩЋЧјгђЕФУцЛ§дНДѓЃЌЪвФкЙтЯпССЖШдНКУ.ЕБ![]() ЮЊЖрЩйЪБЃЌЪвФкЙтЯпССЖШзюКУЃЌВЂЧѓДЫЪБАзЩЋЧјгђЕФУцЛ§.
ЮЊЖрЩйЪБЃЌЪвФкЙтЯпССЖШзюКУЃЌВЂЧѓДЫЪБАзЩЋЧјгђЕФУцЛ§.
ЂкШ§жжДЩзЉЕФЕЅМлСаБэШчЯТЃЌ![]() ОљЮЊе§ећЪ§ЃЌШєЕБ
ОљЮЊе§ећЪ§ЃЌШєЕБ![]() УзЪБЃЌЙКТђШ§ПюДЩзЉЕФзмЗбгУзюЩйЃЌЧвзюЩйЗбгУЮЊ7200дЊЃЌДЫЪБ
УзЪБЃЌЙКТђШ§ПюДЩзЉЕФзмЗбгУзюЩйЃЌЧвзюЩйЗбгУЮЊ7200дЊЃЌДЫЪБ![]() __________ЃЌ
__________ЃЌ
ЁОД№АИЁПЃЈ1ЃЉ8m2;ЃЈ2ЃЉ68m2;(3) 40ЃЌ8
ЁОНтЮіЁП
ЃЈ1ЃЉИљОнжааФЖдГЦЭМаЮаджЪКЭ,![]() ,
,![]() ,
,![]() ПЩЕУ
ПЩЕУ![]() ,МДПЩНтЕБ
,МДПЩНтЕБ![]() ЪБЃЌ4ИіШЋЕШжБНЧШ§НЧаЮЕФУцЛ§ЃЛ
ЪБЃЌ4ИіШЋЕШжБНЧШ§НЧаЮЕФУцЛ§ЃЛ
ЃЈ2ЃЉАзЩЋЧјгђУцЛ§МДЪЧОиаЮУцЛ§МѕШЅвЛЖўВПЗжЕФУцЛ§ЃЌЗжБ№гУКЌxЕФДњЪ§ЪНБэЪОГіСтаЮКЭЫФИіШЋЕШжБНЧШ§НЧаЮЕФУцЛ§ЃЌСаГіКЌгаxЕФНтЮіЪНБэЪОАзЩЋЧјгђУцЛ§ЃЌВЂЛЏГЩЖЅЕуЪНЃЌИљОн![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧѓГіздБфСПЕФШЁжЕЗЖЮЇЃЌдйИљОнЖўДЮКЏЪ§ЕФдіМѕадМДПЩНтД№ЃЛ
ЃЌЧѓГіздБфСПЕФШЁжЕЗЖЮЇЃЌдйИљОнЖўДЮКЏЪ§ЕФдіМѕадМДПЩНтД№ЃЛ
ЃЈ3ЃЉМЦЫуГіx=2ЪБИїВПЗжУцЛ§вдМАгУКЌmЁЂnЕФДњЪ§ЪНБэЪОГіЗбгУЃЌвђЮЊm,nОљЮЊе§ећЪ§ЃЌНтЕУm=40ЃЌn=8.
ЃЈ1ЃЉ Ёп![]() ЮЊГЄЗНаЮКЭСтаЮЕФЖдГЦжааФЃЌ
ЮЊГЄЗНаЮКЭСтаЮЕФЖдГЦжааФЃЌ![]() ЃЌЁр
ЃЌЁр![]()
Ёп![]() ЃЌ
ЃЌ![]() ЃЌЁр
ЃЌЁр![]()
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ЃЌ
ЃЌ![]()
ЃЈ2ЃЉЁп![]() ЃЌ
ЃЌ![]()
Ёр![]() -
- ЃЌ
ЃЌ
Ёп![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()
Ёр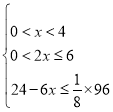 НтВЛЕШЪНзщЕУ
НтВЛЕШЪНзщЕУ![]() ЃЌ
ЃЌ
Ёп![]() ЃЌНсКЯЭМЯёЃЌЕБ
ЃЌНсКЯЭМЯёЃЌЕБ![]() ЪБЃЌ
ЪБЃЌ![]() Ыц
Ыц![]() ЕФдіДѓЖјМѕаЁ.
ЕФдіДѓЖјМѕаЁ.
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ШЁЕУзюДѓжЕЮЊ
ШЁЕУзюДѓжЕЮЊ![]()
ЃЈ3ЃЉЁпЕБ![]() ЪБЃЌSЂё=4x2=16 m2ЃЌ
ЪБЃЌSЂё=4x2=16 m2ЃЌ![]() =12 m2ЃЌ
=12 m2ЃЌ![]() =68m2ЃЌзмЗбгУ:16ЁС2m+12ЁС5n+68ЁС2m=7200,ЛЏМђЕУЃК5n+14m=600,вђЮЊm,nОљЮЊе§ећЪ§ЃЌНтЕУm=40ЃЌn=8.
=68m2ЃЌзмЗбгУ:16ЁС2m+12ЁС5n+68ЁС2m=7200,ЛЏМђЕУЃК5n+14m=600,вђЮЊm,nОљЮЊе§ећЪ§ЃЌНтЕУm=40ЃЌn=8.


 БИеНжаПМКЎМйЯЕСаД№АИ
БИеНжаПМКЎМйЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
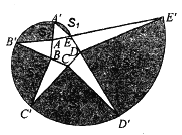
ЁОЬтФПЁПШчЭМЂйЃЌХзЮяЯпyЃНax2+bx+cОЙ§ЕуAЃЈЉ2ЃЌ0ЃЉЁЂBЃЈ4ЃЌ0ЃЉЁЂCЃЈ0ЃЌ3ЃЉШ§ЕуЃЎ
ЃЈ1ЃЉЪдЧѓХзЮяЯпЕФНтЮіЪНЃЛ
ЃЈ2ЃЉЕуPЪЧyжсЩЯЕФвЛИіЖЏЕуЃЌСЌНгPAЃЌЪдЧѓ5PA+4PCЕФзюаЁжЕЃЛ
ЃЈ3ЃЉШчЭМЂкЃЌШєжБЯпlОЙ§ЕуTЃЈЉ4ЃЌ0ЃЉЃЌQЮЊжБЯпlЩЯЕФЖЏЕуЃЌЕБвдAЁЂBЁЂQЮЊЖЅЕуЫљзїЕФжБНЧШ§НЧаЮгаЧвНігаШ§ИіЪБЃЌЪдЧѓжБЯпlЕФНтЮіЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
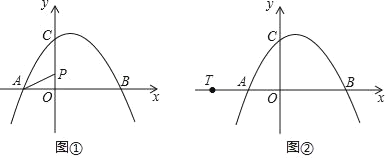
ЁОЬтФПЁПШчЭМЃЌвЛЫвТжДЌКНааЕН B ДІЪБЃЌВтЕУаЁЕК A дкДЌЕФББЦЋЖЋ 60ЁуЕФЗНЯђЃЌТжДЌДг B ДІМЬајЯђе§ЖЋЗНЯђКНаа 20 КЃРяЕНДя C ДІЪБЃЌВтЕУаЁЕК A дкББДЌЕФББЦЋЖЋ 30ЁуЕФЗНЯђЃЎ
ЃЈ1ЃЉШєаЁЕК A ЕНетЫвТжДЌКНааТЗЯп BC ЕФОрРыЪЧ ADЃЌЧѓ AD ЕФГЄЃЎ
ЃЈ2ЃЉвбжЊдкаЁЕКжмЮЇ 17 КЃРяФкгаАЕНИЃЌШєТжДЌВЛИФБфКНЯђМЬајЯђЧАааЪЛЃЌЪдЮЪТжДЌгаЮоДЅНИЕФЮЃЯеЃПЃЈ![]() Ёж1.732ЃЉ
Ёж1.732ЃЉ

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
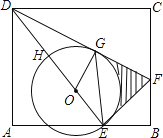
ЁОЬтФПЁПШчЭМЃЌEЪЧГЄЗНаЮABCDЕФБпABЩЯЕФЕуЃЌEFЁЭDEНЛBCгкЕуF
ЃЈ1ЃЉЧѓжЄЃКЁїADEЁзЁїBEFЃЛ
ЃЈ2ЃЉЩшHЪЧEDЩЯвЛЕуЃЌвдEHЮЊжБОЖзїЁбOЃЌDFгыЁбOЯрЧагкЕуGЃЌШєDHЃНOHЃН3ЃЌЧѓЭМжавѕгАВПЗжЕФУцЛ§ЃЈНсЙћБЃСєЕНаЁЪ§ЕуКѓУцЕквЛЮЛЃЌ![]() Ёж1.73ЃЌІаЁж3.14ЃЉЃЎ
Ёж1.73ЃЌІаЁж3.14ЃЉЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌвде§ЮхБпаЮ![]() ЕФЖЅЕу
ЕФЖЅЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїдВЛЁНЛ
ЮЊАыОЖзїдВЛЁНЛ![]() ЕФбгГЄЯпгкЕу
ЕФбгГЄЯпгкЕу![]() ЃЌдйвдЕу
ЃЌдйвдЕу![]() ЮЊдВаФЃЌ
ЮЊдВаФЃЌ![]() ЮЊАыОЖзїдВЛЁНЛ
ЮЊАыОЖзїдВЛЁНЛ![]() ЕФбгГЄЯпгк
ЕФбгГЄЯпгк![]() ЃЌвРДЮНјааЁЁЕУЕНТна§ЯпЃЌдйЫГДЮСЌНс
ЃЌвРДЮНјааЁЁЕУЕНТна§ЯпЃЌдйЫГДЮСЌНс![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЕУЕН5ПщвѕгАЧјгђЃЌШєМЧЫќУЧЕФУцЛ§ЗжБ№ЮЊ
ЃЌЕУЕН5ПщвѕгАЧјгђЃЌШєМЧЫќУЧЕФУцЛ§ЗжБ№ЮЊ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЧвТњзу
ЃЌЧвТњзу![]() ЃЌдђ
ЃЌдђ![]() ЕФжЕЮЊЃЈ ЃЉ
ЕФжЕЮЊЃЈ ЃЉ
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊ![]() a2+10b2+
a2+10b2+![]() c2Љ4abЃН
c2Љ4abЃН![]() aЉ2bcЉ
aЉ2bcЉ![]() ЃЌдђaЉ2b+cЃН_____ЃЎ
ЃЌдђaЉ2b+cЃН_____ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЪ§бЇЩчЭХГЩдБЯыРћгУЫљбЇЕФжЊЪЖВтСПФГЙуИцХЦЕФПэЖШ![]() ЭМжаЯпЖЮMNЕФГЄ
ЭМжаЯпЖЮMNЕФГЄ![]() ЃЌжБЯпMNДЙжБгкЕиУцЃЌДЙзуЮЊЕу
ЃЌжБЯпMNДЙжБгкЕиУцЃЌДЙзуЮЊЕу![]() дкЕиУцAДІВтЕУЕуMЕФбіНЧЮЊ
дкЕиУцAДІВтЕУЕуMЕФбіНЧЮЊ![]() ЁЂЕуNЕФбіНЧЮЊ
ЁЂЕуNЕФбіНЧЮЊ![]() ЃЌдкBДІВтЕУЕуMЕФбіНЧЮЊ
ЃЌдкBДІВтЕУЕуMЕФбіНЧЮЊ![]() ЃЌ
ЃЌ![]() УзЃЌЧвAЁЂBЁЂPШ§ЕудквЛжБЯпЩЯ
УзЃЌЧвAЁЂBЁЂPШ§ЕудквЛжБЯпЩЯ![]() ЧыИљОнвдЩЯЪ§ОнЧѓЙуИцХЦЕФПэMNЕФГЄЃЎ
ЧыИљОнвдЩЯЪ§ОнЧѓЙуИцХЦЕФПэMNЕФГЄЃЎ
![]() ВЮПМЪ§ОнЃК
ВЮПМЪ§ОнЃК![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]()

ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
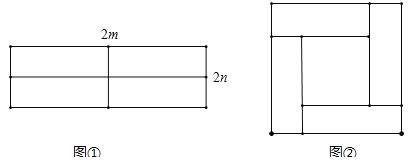
ЁОЬтФПЁПШчЭМЃЌЭМЂйЫљЪОЪЧвЛИіГЄЮЊ2mЃЌПэЮЊ2nЕФГЄЗНаЮЃЌгУМєЕЖОљЗжГЩЫФИіаЁГЄЗНаЮЃЌШЛКѓАДЭМЂкЕФЗНЪНЦДГЩвЛИіДѓе§ЗНаЮЃЎ
ЃЈ1ЃЉЭМЂкжаЕФДѓе§ЗНаЮЕФБпГЄЕШгкЁЁ ЁЁЃЌЭМЂкжаЕФаЁе§ЗНаЮЕФБпГЄЕШгкЁЁ ЁЁЃЛ
ЃЈ2ЃЉЭМЂкжаЕФДѓе§ЗНаЮЕФУцЛ§ЕШгкЁЁ ЁЁЃЌЭМЂкжаЕФаЁе§ЗНаЮЕФУцЛ§ЕШгкЁЁ ЁЁЃЛЭМЂйжаУПИіаЁГЄЗНаЮЕФУцЛ§ЪЧЁЁ ЁЁЃЛ
ЃЈ3ЃЉЙлВьЭМЂкЃЌФуФмаДГіЃЈm+nЃЉ2ЃЌЃЈmЉnЃЉ2ЃЌmnетШ§ИіДњЪ§ЪНМфЕФЕШСПЙиЯЕТ№ЃПЁЁ ЁЁЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌе§ЗНаЮABCDжаЃЌЕуEЁЂFЗжБ№дкЯпBCЁЂCDЩЯдЫЖЏЃЌЧвТњзуЁЯEAFЃН45ЁуЃЌAEЁЂAFЗжБ№гыBDЯрНЛгкЕуMЁЂNЃЎЯТСаЫЕЗЈжаЃКЂйBE+DFЃНEFЃЛЂкЕуAЕНЯпЖЮEFЕФОрРывЛЖЈЕШгке§ЗНаЮЕФБпГЄЃЛЂлШєtanЁЯBAEЃН![]() ЃЌдђtanЁЯDAFЃН
ЃЌдђtanЁЯDAFЃН![]() ЃЛЂмШєBEЃН2ЃЌDFЃН3ЃЌдђSЁїAEFЃН18ЃЎЦфжаНсТле§ШЗЕФЪЧ__ЃЈНЋе§ШЗЕФађКХаДдкКсЯпЩЯЃЉ
ЃЛЂмШєBEЃН2ЃЌDFЃН3ЃЌдђSЁїAEFЃН18ЃЎЦфжаНсТле§ШЗЕФЪЧ__ЃЈНЋе§ШЗЕФађКХаДдкКсЯпЩЯЃЉ

ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com