
【题目】已知四边形![]() 为
为![]() 的内接四边形,直径
的内接四边形,直径![]() 与对角线
与对角线![]() 相交于点
相交于点![]() ,作
,作![]() 于
于![]() ,
,![]() 与过
与过![]() 点的直线相交于点
点的直线相交于点![]() ,
,![]() .
.
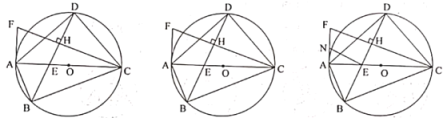
(1)求证:![]() 为
为![]() 的切线;
的切线;
(2)若![]() 平分
平分![]() ,求证:
,求证:![]() ;
;
(3)在(2)的条件下,![]() 为
为![]() 的中点,连接
的中点,连接![]() ,若
,若![]() ,
,![]() 的半径为
的半径为![]() ,求
,求![]() 的长.
的长.
【答案】(1)证明见解析(2)证明见解析(3)![]()
【解析】
(1)根据直径所对的圆周角为90°,得到∠ADC=90°,根据直角三角形两锐角互余得到∠DAC+∠DCA=90°,再根据同弧或等弧所对的圆周角相等,可得到∠FAD+∠DAC=90°,即可得出结论;
(2)连接OD.根据圆周角定理和角平分线定义可得∠DOA=∠DOC,即可得出结论;
(3)连接OD交CF于M,作EP⊥AD于P.可求出AD=4,AF∥OM.根据三角形中位线定理得出OM=![]() AF.证明△ODE≌△OCM,得到OE=OM.设OM=m,用m表示出OE,AE,AP,DP.通过证明△EAN∽△DPE,根据相似三角形对应边成比例,求出m的值,从而求得AN,AE的值.在Rt△NAE中,由勾股定理即可得出结论.
AF.证明△ODE≌△OCM,得到OE=OM.设OM=m,用m表示出OE,AE,AP,DP.通过证明△EAN∽△DPE,根据相似三角形对应边成比例,求出m的值,从而求得AN,AE的值.在Rt△NAE中,由勾股定理即可得出结论.
(1)∵AC为⊙O的直径,
∴∠ADC=90°,
∴∠DAC+∠DCA=90°.
∵![]() ,
,
∴∠ABD=∠DCA.
∵∠FAD=∠ABD,
∴∠FAD=∠DCA,
∴∠FAD+∠DAC=90°,
∴CA⊥AF,
∴AF为⊙O的切线.

(2)连接OD.
∵![]() ,
,
∴∠ABD=![]() ∠AOD.
∠AOD.
∵![]() ,
,
∴∠DBC=![]() ∠DOC.
∠DOC.
∵BD平分∠ABC,
∴∠ABD=∠DBC,
∴∠DOA=∠DOC,
∴DA=DC.

(3)连接OD交CF于M,作EP⊥AD于P.
∵AC为⊙O的直径,
∴∠ADC=90°.
∵DA=DC,
∴DO⊥AC,
∴∠FAC=∠DOC=90°,AD=DC=![]() =4,
=4,
∴∠DAC=∠DCA=45°,AF∥OM.
∵AO=OC,
∴OM=![]() AF.
AF.
∵∠ODE+∠DEO=90°,∠OCM+∠DEO=90°,
∴∠ODE=∠OCM.
∵∠DOE=∠COM,OD=OC,
∴△ODE≌△OCM,
∴OE=OM.
设OM=m,
∴OE=m,![]() ,
,![]() ,
,
∴![]() .
.
∵∠AED+∠AEN=135°,∠AED+∠ADE=135°,
∴∠AEN=∠ADE.
∵∠EAN=∠DPE,
∴△EAN∽△DPE,
∴![]() ,
,
∴ ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
由勾股定理得:![]() .
.



 能力评价系列答案
能力评价系列答案 唐印文化课时测评系列答案
唐印文化课时测评系列答案科目:初中数学 来源: 题型:
【题目】丽江布农铃,是一种极富特色的、形状同马帮的马铃的挂件.这种马帮文化商品,是纯手工制作.精致小巧的青铜铃铛下系有一块圆形木块,手绘着各种各样的画.某商店需要购进甲、乙两种布农铃共300件,一件甲种布农铃进价为340元,售价为400元,一件乙种布农铃进价为380元,售价为460元.(注:利润=售价-进价)
(1)若商店计划销售完这批布农铃后能获利21600元,问甲、乙两种布农铃应分别购进多少件?
(2)若商店计划投入资金110000元,则能购进甲种布农铃多少件?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,对角线AC=2![]() ,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,点B恰好落在对角线AC上的点B′处,P,Q分别是AB,AC上的动点,则PE+PQ的最小值为( )
,E为BC边上一点,BC=3BE,将矩形ABCD沿AE所在的直线折叠,点B恰好落在对角线AC上的点B′处,P,Q分别是AB,AC上的动点,则PE+PQ的最小值为( )
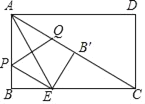
A.![]() B.2C.1D.3
B.2C.1D.3
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】二次函数![]() (a≠0)的图象如图所示,则下列命题中正确的是( )
(a≠0)的图象如图所示,则下列命题中正确的是( )
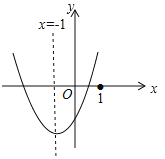
A. a >b>c
B. 一次函数y=ax +c的图象不经第四象限
C. m(am+b)+b<a(m是任意实数)
D. 3b+2c>0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数y1=![]() 的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).
的图象与一次函数y2=ax+b的图象相交于点A(1,4)和B(﹣2,n).

(1)求反比例函数与一次函数的解析式;
(2)请根据图象直接写出y1<y2时,x的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
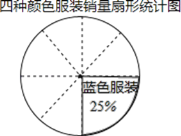
【题目】某超市销售多种颜色的运动服装,其中平均每天销售红、黄、蓝、白四种颜色运动服的数量如表,由此绘制的不完整的扇形统计图如图:
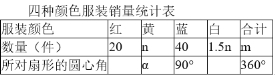
(1)求表中m、n、α的值,并将扇形统计图补充完整:表中m= ,n= ,α= ;
(2)为吸引更多的顾客,超市将上述扇形统计图制成一个可自由转动的转盘,并规定:顾客在本超市购买商品金额达到一定的数目,就获得一次转动转盘的机会.如果转盘停止后,指针指向红色服装区域、黄色服装区域,可分别获得60元、20元的购物券.求顾客每转动一次转盘获得购物券金额的平均数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,已知直线y=-2x+4与x轴、y轴分别交于点A、C,以OA、OC为边在第一象限内作长方形OABC.

(1)求点A、C的坐标;
(2)将△ABC对折,使得点A的与点C重合,折痕交AB于点D,求直线CD的解析式(图②);
(3)在坐标平面内,是否存在点P(除点B外),使得△APC与△ABC全等?若存在,请直接写出所有符合条件的点P的坐标;若不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com