��������1������һ���ȸ���ֱ��y=2x+4�����A��B�����꣬�Ӷ��õ�OA��OB�ij��ȣ��ٸ���ƽ���ı��εĶԱ�������BC�ij��ȣ�����C��CK��x����K���Ӷ��õ��ı���BOKC�Ǿ��Σ����ݾ��εĶԱ�������KC�ij��ȣ��Ӷ��õ���C�����꣬Ȼ��ѵ�C���������ֱ�������m��ֵ��
���������ȸ���ֱ��y=2x+4�����A��B�����꣬�Ӷ��õ�OA��OB�ij��ȣ����ӳ�DC��y���ڵ�N������ֱ��y=-x+m���D��N�����꣬���õ�OD=ON���Ӷ��õ���ODN=��OND=45�㣬�ٸ���ƽ���ı��εĶԱ���õ�BC=OA=2�����ݶԱ�ƽ�еõ�BC��AO��Ȼ�������BN=BC=2�����ON�ij��ȣ���Ϊֱ��y=-x+m��m��ֵ��
��2������һ���ӳ�DC��y����N�ֱ����E��G��x��Ĵ��� ����ֱ���R��Q���ı���ERQG���ı���POQG���ı���EROP�Ǿ��Σ������á�BAO������ֵ���AR�ij��ȣ����á�ODN������ֵ���DQ�ij��ȣ�������AD�ij��ȼ�ȥAR�ij��ȣ��ټ�ȥDQ�ij��ȣ����㼴�ɵý⣻
������������ֱ��AB�Ľ���ʽ�����E�ĺ����꣬����ֱ��CD�Ľ���ʽ�����G�ĺ����꣬�õ�G�ĺ������ȥ��E�ĺ����꣬���㼴�ɵý⣻
��3������һ������ƽ���ı��εĶԱ�ƽ�пɵ�AB��OC���ٸ�����ֱ��ƽ�У��ڴ�����������ABO=��BOC����t��ʾ��BP���ٸ��ݡ�ABO���BOC������ֵ�����ʽ���EP�ij��ȣ��ٱ�ʾ��PG�ij��ȣ�Ȼ�����ֱ�����Ե�Բ�ܽ���ֱ�ǿɵá�OMC=90�㣬����ֱ���Ƴ���BGP=��BOC�������á�BGP���BOC������ֵ�����ʽ��⼴�ɵõ�t��ֵ���ȸ��ݼӵĹ�ϵ�����OBF=��FBH�����ж���BHF�͡�BFO���ƣ��������������ζ�Ӧ�߳ɱ����ɵ�
=
���ٸ���t=2���OP=2��PF=1��BP=2�����ù��ɶ������BF�ij��ȣ��������ݽ��м��㼴�����BH��ֵ��Ȼ�����HO��ֵ���Ӷ��õ���H�����ꣻ
��������ͬ����һ���t=2��Ȼ�����OP=2��BP=2�������PF=1�����ݹ��ɶ������OF��BF�ij�����ȣ�������
�����ݵȱ߶ԵȽǵ����ʿɵá�OBF=��BOC=��BFH=��ABO���ٸ��ݵȽǶԵȱߵ����ʿɵ�BH=HF��Ȼ�����H��HT��BF�ڵ�T�����á�OBF���������õ�BH��Ȼ�����HO��ֵ���Ӷ��õ���H�����ꣻ
�����������ɹ��ɶ������AB�ij��ȣ�Ȼ����t��ʾ��BP���ٸ��ݡ�ABO��������ʽ���BE�ij��ȣ�����ֱ�����Ե�Բ�ܽ���ֱ�ǿɵá�OMG=90�㣬Ȼ�����ͬ�ǵ������ȿɵá�ABO=��BGE���ٸ��ݡ�ABO�͡�BGE������ֵ�����ʽ��⼴�ɵõ�t=2���±�����뷽��һ��ͬ��
�����1���⣺����һ����ͼ1����y=2x+4��x���y����A��B��
��A��-2��0��B��0��4����
��OA=2��OB=4��
���ı���ABCO��ƽ���ı��Σ�
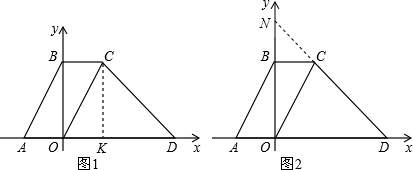
��BC=OA=2 ����C��CK��x����K��
���ı���BOKC�Ǿ��Σ�
��OK=BC=2��CK=OB=4��
��C��2��4������y=-x+m�ã�4=-2+m��
��m=6��
����������ͼ2����y=2x+4��x���y����A��B��
��A��-2��0��B��0��4����
��OA=2 OB=4��
�ӳ�DC��y���ڵ�N��
��y=-x+m��x���y���ڵ�D��N��
��D��m��0��N��0��m����
��OD=ON��
���ODN=��OND=45�㣬
���ı���ABCO��ƽ���ı��Σ�
��BC��AO��BC=OA=2��
���NCB=��ODN=��OND=45�㣬
��NB=BC=2��
��ON=NB+OB=2+4=6��
��m=6��
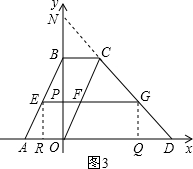
��2���⣺����һ����ͼ3���ӳ�DC��y����N�ֱ����E��G��x��Ĵ��� ����ֱ���R��Q���ı���ERQG���ı���POQG���ı���EROP�Ǿ��Σ�
��ER=PO=GQ=t��
��tan��BAO=
=
��
��
=
��
��AR=
t
��
��y=-x+6��x���y����D��N��
��OD=ON=6��
���ODN=45�㣬
��tan��ODN=
��
��DQ=t��
�֡�AD=AO+OD=2+6=8��
��EG=RQ=8-
t-t=8-
t��
��d=-
t+8��0��t��4����
����������ͼ4����EG��AD��P��O��t����
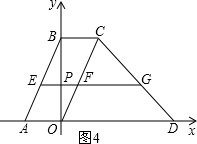
����E��x
1��t����G��x
2��t����
��E��x
1��t������y=2x+4��t=2x
1+4��
��x
1=
-2��
��G��x
2��t������y=-x+6��t=-x
2+6��
��x
2=6-t��
��d=EG=x
2-x
1=��6-t��-��
-2��=8-
t��
��d=-
t+8��0��t��4����
��3���⣺����һ����ͼ5�����ı���ABCO��ƽ���ı��Σ�
��AB��OC��
���ABO=��BOC��
��BP=4-t��
��tan��AB0=
=tan��BOC=
��
��EP=2-
��
��PG=d-EP=6-t��
����OGΪֱ����Բ������M��
���OMG=90�㣬��MFG=��PFO��
���BGP=��BOC��
��tan��BGP=
=tan��BOC=
��

��
=
��
���t=2��
�ߡ�BFH=��ABO=��BOC����OBF=��FBH��
���BHF�ס�BFO��
��
=
��
��BF
2=BH•BO��
��OP=2��
��PF=1��BP=2��
��BF=
=
��
��5=BH��4��
��BH=
��
��HO=4-
=
��
��H��0��
����
����������ͼ6�����ı���ABCO��ƽ���ı��Σ�
��AB��OC��
���ABO=��BOC��
��BP=4-t��
��tan��AB0=
=tan��BOC=
��
��EP=2-
��
��PG=d-EP=6-t��
����OGΪֱ����Բ������M��
���OMG=90�㣬��MFG=��PFO��
���BGP=��BOC��
��tan��BGP=
=tan��BOC=
��
��
=
��
���t=2��
��OP=2��BP=4-t=2��
��PF=1��
��OF=
=
=BF��
���OBF=��BOC=��BFH=��ABO��
��BH=HF��
����H��HT��BF�ڵ�T��
��BT=
BF=
��
��BH=
=
=
��
��OH=4-
=
��
��H��0��
����
����������ͼ7����OA=2��OB=4��
���ɹ��ɶ����ã�AB=2
��
��P��O��t����
��BP=4-t��

��cos��ABO=
=
=
=
��
��BE=
��4-t����
����OGΪֱ����Բ������M��
���OMG=90�㣬
���ı���ABCO��ƽ���ı��Σ�
��AB��OC��
���ABG=��OMG=90��=��BPG��
���ABO+��BEG=90�㣬��BGE+��BEG=90�㣬
���ABO=��BGE��
��sin��ABO=sin��BGE��
��
=
=
��
��
=
��
��t=2��
�ߡ�BFH=��ABO=BOC����OBF=��FBH��
���BHF�ס�BFO��
��
=
��
��BF
2=BH•BO��
��OP=2��
��PF=1��BP=2��
��BF=
=
��
��5=BH��4��
��BH=
��
��OH=4-
=
��
��H��0��
����
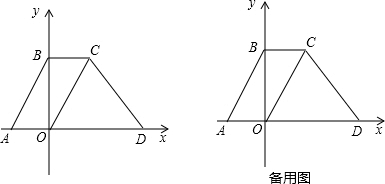
�����������Ƕ�һ�κ������ۺϿ��飬��Ҫ������ֱ����������Ľ������⣬ƽ���ı��εĶԱ�ƽ������ȵ����ʣ����������ε��ж������ʣ����ɶ�����ֱ�����Ե�Բ�ܽ���ֱ�ǵ����ʣ���ֱ�������ε�Ӧ�ã��ۺ��Խ�ǿ���ѶȽϴ��ݲ�ͬ��˼·�������ҵ���ͬ����ⷽ����һ���⣬��һ������ϣ��ͬѧ�������о�����ϸ��ĥ��


 ��
��




 Сѧ���AB��ϵ�д�
Сѧ���AB��ϵ�д�
 ��2012•����������ͼ��ʾ�ļ�������������С��������϶��ɵģ���������ͼ�ǣ�������
��2012•����������ͼ��ʾ�ļ�������������С��������϶��ɵģ���������ͼ�ǣ�������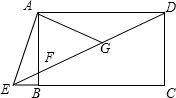 ��2012•����������ͼ���ı���ABCD�Ǿ��Σ���E���߶�CB���ӳ����ϣ�����DE��AB�ڵ�F����AED=2��CED����G��DF���е㣬��BE=1��AG=4����AB�ij�Ϊ
��2012•����������ͼ���ı���ABCD�Ǿ��Σ���E���߶�CB���ӳ����ϣ�����DE��AB�ڵ�F����AED=2��CED����G��DF���е㣬��BE=1��AG=4����AB�ij�Ϊ