
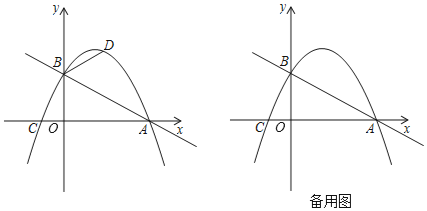
【题目】如图,在平面直角坐标系中,直线![]() 与x轴交于点
与x轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]() ,抛物线
,抛物线![]() 经过
经过![]() 两点且与x轴的负半轴交于点
两点且与x轴的负半轴交于点![]() .
.
![]() 求该抛物线的解析式;
求该抛物线的解析式;
![]() 若点
若点![]() 为直线
为直线![]() 上方抛物线上的一个动点,当
上方抛物线上的一个动点,当![]() 时,求点
时,求点![]() 的坐标;
的坐标;
![]() 已知
已知![]() 分别是直线
分别是直线![]() 和抛物线上的动点,当
和抛物线上的动点,当![]() 为顶点的四边形是平行四边形时,直接写出所有符合条件的
为顶点的四边形是平行四边形时,直接写出所有符合条件的![]() 点的坐标.
点的坐标.
【答案】(1)![]() (2)点
(2)点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()
【解析】
![]() 求得
求得![]() 两点坐标,代入抛物线解析式,获得
两点坐标,代入抛物线解析式,获得![]() 的值,获得抛物线的解析式.
的值,获得抛物线的解析式.
![]() 通过平行线分割
通过平行线分割![]() 倍角条件,得到相等的角关系,利用等角的三角函数值相等,得到点坐标.
倍角条件,得到相等的角关系,利用等角的三角函数值相等,得到点坐标.
![]() 四点作平行四边形,以已知线段
四点作平行四边形,以已知线段![]() 为边和对角线分类讨论,当
为边和对角线分类讨论,当![]() 为边时,以
为边时,以![]() 的关系建立方程求解,当
的关系建立方程求解,当![]() 为对角线时,
为对角线时,![]() 与
与![]() 互相平分,利用直线相交获得点
互相平分,利用直线相交获得点![]() 坐标.
坐标.
![]() 在
在![]() 中,令
中,令![]() ,得
,得![]() ,令
,令![]() ,得
,得![]()
![]()
把![]() ,代入
,代入![]() ,得
,得
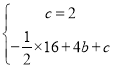 ,解得
,解得![]()
![]() 抛物线得解析式为
抛物线得解析式为![]()
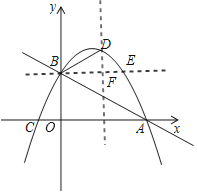
![]() 如图,过点
如图,过点![]() 作
作![]() 轴得平行线交抛物线于点
轴得平行线交抛物线于点![]() ,过点
,过点![]() 作
作![]() 得垂线,垂足为
得垂线,垂足为![]()
![]() 轴,
轴,
![]()
![]()
![]()
即![]()
![]()
![]()
设![]() 点的坐标为
点的坐标为 ![]() ,则
,则![]()
![]() ,
,![]()
![]() ,即
,即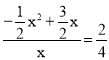
解得![]() (舍去),
(舍去),![]()
当![]() 时,
时,![]()
![]() 点
点![]() 的坐标为
的坐标为![]()
![]() 当
当![]() 为边时,
为边时, ![]()
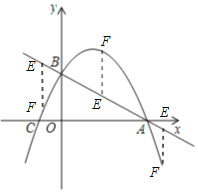
设 ![]()
![]()
解得 ![]()
当![]() 为对角线时,
为对角线时,![]() 与
与![]() 互相平分
互相平分
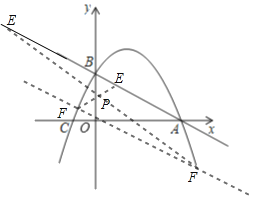
过点![]() 作
作![]() ,直线
,直线![]() 交抛物线于点
交抛物线于点![]() ,
,![]()
求得直线![]() 解析式为
解析式为![]()
直线![]() 与
与![]() 的交点为
的交点为![]() ,点
,点![]() 的横坐标为
的横坐标为![]() 或
或![]()
![]() 点的坐标为
点的坐标为![]() 或
或![]() 或
或![]() 或
或![]() 或
或![]()


 99加1领先期末特训卷系列答案
99加1领先期末特训卷系列答案 百强名校期末冲刺100分系列答案
百强名校期末冲刺100分系列答案 好成绩1加1期末冲刺100分系列答案
好成绩1加1期末冲刺100分系列答案 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:初中数学 来源: 题型:
【题目】某市政府为了鼓励居民节约用水,计划调整居民生活用水收费方案:一户家庭的月均用水量不超过![]() (单位:
(单位:![]() )的部分按平价收费,超出
)的部分按平价收费,超出![]() 的部分按议价收费.为此拟召开听证会,以确定一个合理的月均用水量标准
的部分按议价收费.为此拟召开听证会,以确定一个合理的月均用水量标准![]() .通过抽样,获得了前一年1000户家庭每户的月均用水量(单位:
.通过抽样,获得了前一年1000户家庭每户的月均用水量(单位:![]() ),将这1000个数据按照
),将这1000个数据按照![]() ,
,![]() ,…,
,…,![]() 分成8组,制成了如图所示的频数分布直方图.
分成8组,制成了如图所示的频数分布直方图.
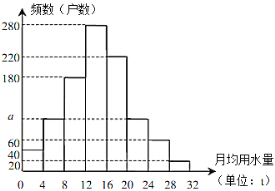
(1)写出![]() 的值,并估计这1000户家庭月均用水量的平均数;(同一组中的数据以这组数据所在范围的组中值作代表)
的值,并估计这1000户家庭月均用水量的平均数;(同一组中的数据以这组数据所在范围的组中值作代表)
(2)假定该市政府希望70%的家庭的月均用水量不超过标准![]() ,请判断若以(1)中所求得的平均数作为标准
,请判断若以(1)中所求得的平均数作为标准![]() 是否合理?并说明理由.
是否合理?并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(抗击疫情)为了遏制新型冠状病毒疫情的蔓延势头,各地教育部门在推迟各级学校开学时间的同时提出“听课不停学”的要求,各地学校也都开展了远程网络教学,某校集中为学生提供四类在线学习方式:在线阅读、在线听课、在线答疑、在线讨论,为了了解学生的需求,该校通过网络对本校部分学生进行了“你对哪类在线学习方式最感兴趣”的调查,并根据结果绘制成如下两幅不完整的统计图。

(1)本次调查的人数有多少人?
(2)请补全条形图;
(3)请求出“在线答疑”在扇形图中的圆心角度数;
(4)小宁和小娟都参加了远程网络教学活动,请求出小宁和小娟选择同一种学习方式的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】随着时代的不断发展,新颖的网络购进逐渐融入到人们的生活中,“拼一拼”电商平台上提供了一种拼团购买方式,当拼团(单数不超过15单)成功后商家将会让利一定的额度给予顾客实惠.现在某商家准备出手一种每件成本25元/件的新产品,经市场调研发现,单价y(单位:元)、日销售量m(单位:件)与拼单数x(单位:单)之间存在着如表的数量关系:
拼单数x(单位:单) | 2 | 4 | 8 | 12 |
单价y(单位:元) | 34.50 | 34.00 | 33.00 | 32.00 |
日销售量m(单位:件) | 68 | 76 | 92 | 108 |
请根据以上提供的信息解决下列问题:
(1)请直接写出单价y和日销售量m分别与拼单数x之间的一次函数关系式;
(2)拼单数设置为多少单时的日销售利润最大,最大的销售利润是多少?
(3)在实际销售过程中,厂家希望能有更多的商品出售,因此对电商每销售一件商品厂家就给予电商补助a元(a≤2),那么电商在获得补助之日后日销售利润能够随单数x的增大而增大,那么a的取值范围是什么?
查看答案和解析>>
科目:初中数学 来源: 题型:
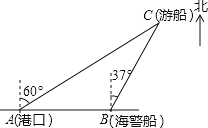
【题目】 一艘观光游船从港口A以北偏东60°的方向出港观光,航行80海里至C处时发生了侧翻沉船事故,立即发出了求救信号,一艘在港口正东方向的海警船接到求救信号,测得事故船在它的北偏东37°方向,马上以40海里每小时的速度前往救援,求海警船到大事故船C处所需的大约时间.(温馨提示:sin53°≈0.8,cos53°≈0.6)
查看答案和解析>>
科目:初中数学 来源: 题型:
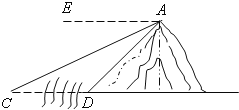
【题目】如图,河旁有一座小山,从山顶A处测得河对岸点C的俯角为30°,测得岸边点D的俯角为45°,现从山顶A到河对岸点C拉一条笔直的缆绳AC,如果AC是120米,求河宽CD的长?
查看答案和解析>>
科目:初中数学 来源: 题型:
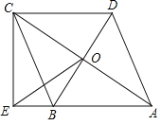
【题目】如图,在四边形ABCD中,对角线AC、BD交于点O,AB∥DC,AB=BC,BD平分∠ABC,过点C作CE⊥AB交AB的延长线于点E,连接OE.
(1)求证:四边形ABCD是菱形;
(2)若AB=2![]() ,BD=4,求OE的长.
,BD=4,求OE的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com