
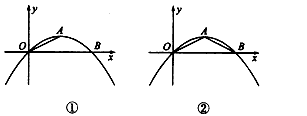
| 解:(1)∵此抛物线过原点(0,0), ∴设y=ax2+bx, 将A代入得, ∴1=4a+2b, ∵A(2,1)为顶点, ∴ 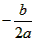 =2, =2,∴b=-4a, ∴1=4a+2×(-4a)=-4a, ∴a=-  , ,∴b=1, ∴y=- 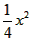 +x; +x; |
|
| (2)∵y=-x平分∠AOM,∠FOE=∠HOE=45°, ∴∠1=∠2,如图①,作AE⊥OA,EN⊥ON(E在y=-x上), ∴ON=OA,作AR⊥x,NS⊥y, ∴∠ORA=∠OSN=90°,且AR=1,OR=2, 在△OAR与△ONS中, 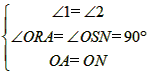 ∴△OAR≌△ONS(AAS) ∴AR=NS=1,OR=OS=2, ∴N(-1,-2), ∴l∶ON,y=2x M即为ON与抛物线交点, ∴ 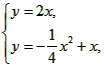 ∴ 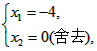 ∴M(-4,-8); |
 |
| (3)当△OAB∽△OBP时, ∠AOB=∠BOP, ∴OB平分∠AOP或∠ABP, ∴l:OP1必过点(2.-1), ∴1∶OP1,y= 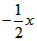 ∴ 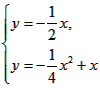 ∴ 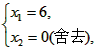 ∴P1(6,-3), ∴l:BP2必过点(2,-1), ∴l:BP2,y= 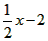 ∴ 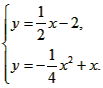 ∴ 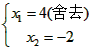 ∴P2(-2,-3), 如图②,连OP2,BP1,作P2Q⊥y轴, ∴P2Q =2,OQ=3, 在Rt△OP2Q中,OP2= 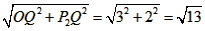 , ,由抛物线对称性得OP2=BP1= 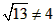 ∴OP2≠OB,BP1≠ OB, ∴不存在P点(抛物线上)使△OBP与△OAB相似。 |
 |


 智趣暑假温故知新系列答案
智趣暑假温故知新系列答案 英语小英雄天天默写系列答案
英语小英雄天天默写系列答案科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
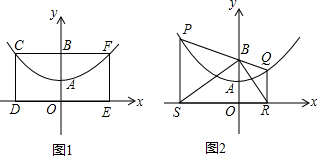
 轴上,CF交y轴于点B(0,2),且其面积为8.
轴上,CF交y轴于点B(0,2),且其面积为8.查看答案和解析>>
科目:初中数学 来源: 题型:
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com