
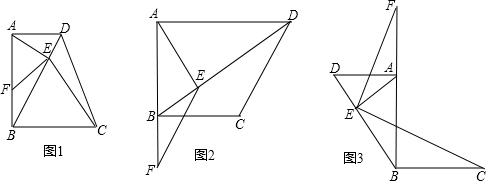
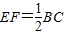 ;将AC沿BC方向平移到DH,得图(2),沿CB方向平移到DH得图(3),图(2)中AD与BH存在关系:EF∥AD,
;将AC沿BC方向平移到DH,得图(2),沿CB方向平移到DH得图(3),图(2)中AD与BH存在关系:EF∥AD, ;,那么在图(3)中是否有类似于图(1)(2)中的结论,请把猜想的结论填在方框内,并就图(3)的结论加以证明.
;,那么在图(3)中是否有类似于图(1)(2)中的结论,请把猜想的结论填在方框内,并就图(3)的结论加以证明.
 BH,再根据平移可知四边形ADCH是平行四边形,且FG∥BC,从而得到FG=
BH,再根据平移可知四边形ADCH是平行四边形,且FG∥BC,从而得到FG= (AD+CH),最后根据EF=EG-FG整理即可得解;
(AD+CH),最后根据EF=EG-FG整理即可得解; ,
,
 BC;
BC; BH,
BH, (AD+CH),
(AD+CH), BH-
BH- (AD+CH)=
(AD+CH)= (BH-CH)-
(BH-CH)- AD=
AD= (BC-AD);
(BC-AD); BH,
BH, (AD+CH),
(AD+CH), BH+
BH+ (AD+CH)=
(AD+CH)= (BH+CH)+
(BH+CH)+ AD=
AD= (BC+AD).
(BC+AD).

 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案科目:初中数学 来源: 题型:
| 3 | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
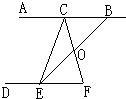 28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.
28、如图,C、E分别在AB、DF上,小华想知道∠ACE和∠DEC是否互补,但是他有没有带量角器,只带了一副三角尺,于是他想了这样一个办法:首先连接CF,再找出CF的中点O,然后连接EO并延长EO和直线AB相交于点B,经过测量,他发现EO=BO,因此他得出结论:∠ACE和∠DEC互补,而且他还发现BC=EF.以下是他的想法,请你填上根据.查看答案和解析>>
科目:初中数学 来源: 题型:
| AE |
| BE |
| ED |
| BE |
查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com