
【题目】如图,在坐标系中放置一菱形![]() ,已知
,已知![]() ,
,![]() ,先将菱形
,先将菱形![]() 沿
沿![]() 轴的正方向无滑动翻转,每次翻转
轴的正方向无滑动翻转,每次翻转![]() ,连续翻转2019次,点
,连续翻转2019次,点![]() 的落点依次为
的落点依次为![]() ,
,![]() ,
,![]() ,…,则
,…,则![]() 的坐标为__________.
的坐标为__________.
【答案】(1346,0)
【解析】
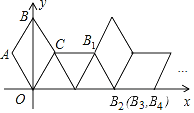
根据题意连接AC,根据条件可以求出AC,画出第5次、第6次、第7次翻转后的图形,容易发现规律:每翻转6次,图形向右平移4.由于2019=336×6+3,因此点![]() 向右平移1344(即336×4)即可到达点
向右平移1344(即336×4)即可到达点![]() ,根据点
,根据点![]() 的坐标就可求出点
的坐标就可求出点![]() 的坐标.
的坐标.
解:连接AC,如图所示:
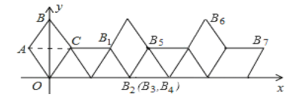
∵四边形OABC是菱形,
∴OA=AB=BC=OC.
∵∠ABC=60°,
∴△ABC是等边三角形.
∴AC=AB.
∴AC=OA.
∵OA=1,
∴AC=1.
画出第5次、第6次、第7次翻转后的图形,如上图所示.
由图可知:每翻转6次,图形向右平移4.
∵2019=336×6+3,
∴点![]() 向右平移1344(即336×4)到点
向右平移1344(即336×4)到点![]() .
.
∵![]() 的坐标为(2,0),
的坐标为(2,0),
∴![]() 的坐标为(2+1344,0),
的坐标为(2+1344,0),
∴![]() 的坐标为(1346,0).
的坐标为(1346,0).
故答案为:(1346,0).


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
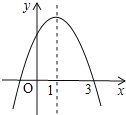
【题目】已知二次函数y=ax2+bx+c的图象如图所示,对称轴为直线x=1,则下列结论①abc>0②方程ax2+bx+c=0的两个根是x1=﹣1,x2=3③4a+2b+c<0④当x>0时,y随x的增大而减小正确的是( ).
A.①③④B.②④C.①②③D.②
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边三角形ABC中,点P是BC边上一动点(不与点B、C重合),连接AP,作射线PD,使∠APD=60°,PD交AC于点D,已知AB=a,设CD=y,BP=x,则y与x函数关系的大致图象是( )

A. 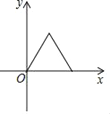 B.
B. 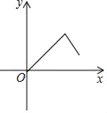 C.
C.  D.
D. 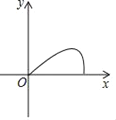
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等边△ABC,点D为BC上一点,连接AD.
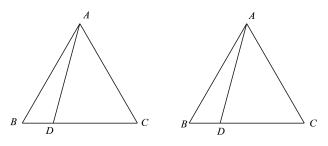
图1 图2
(1)若点E是AC上一点,且CE=BD,连接BE,BE与AD的交点为点P,在图(1)中根据题意补全图形,直接写出∠APE的大小;
(2)将AD绕点A逆时针旋转120°,得到AF,连接BF交AC于点Q,在图(2)中根据题意补全图形,用等式表示线段AQ和CD的数量关系,并证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,抛物线
中,抛物线![]() 与
与![]() 轴的交点为A,B(点A 在点B的左侧).
轴的交点为A,B(点A 在点B的左侧).
(1)求点A,B的坐标;
(2)横、纵坐标都是整数的点叫整点.
①直接写出线段AB上整点的个数;
②将抛物线![]() 沿
沿![]() 翻折,得到新抛物线,直接写出新抛物线在
翻折,得到新抛物线,直接写出新抛物线在![]() 轴上方的部分与线段
轴上方的部分与线段![]() 所围成的区域内(包括边界)整点的个数.
所围成的区域内(包括边界)整点的个数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 经过点
经过点![]() 、
、![]() ,且与
,且与![]() 轴交于点
轴交于点![]() ,抛物线的顶点为
,抛物线的顶点为![]() ,连接
,连接![]() ,点
,点![]() 是线段
是线段![]() 上的一个动点(不与
上的一个动点(不与![]() 、
、![]() )重合.
)重合.
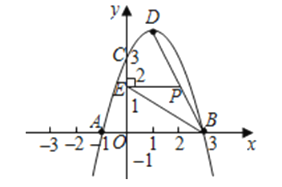
(1)求抛物线的解析式,并写出顶点![]() 的坐标;
的坐标;
(2)过点![]() 作
作![]() 轴于点
轴于点![]() ,求
,求![]() 面积的最大值及取得最大值时
面积的最大值及取得最大值时![]() 点的坐标;
点的坐标;
(3)在(2)的条件下,若点![]() 是
是![]() 轴上一动点,点
轴上一动点,点![]() 是抛物线上一动点,试判断是否存在这样的点
是抛物线上一动点,试判断是否存在这样的点![]() ,使得以点
,使得以点![]() ,
,![]() ,
,![]() ,
,![]() 为顶点的四边形是平行四边若存在,请直接写出点
为顶点的四边形是平行四边若存在,请直接写出点![]() 的坐标:若不存在,请说明理由.
的坐标:若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】问题:如图1,在平行四边形ABCD中,点E是BC边的中点,连结AE,点F是线段AE上一点,连结BF并延长,交射线CD于点G.若AF:EF=4:1,求![]() 的值.
的值.
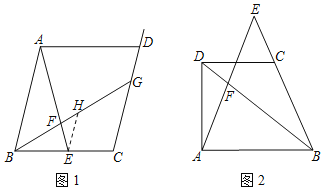
(1)尝试探究:
如图1,过点E作EH∥AB交BG于点H,则AB和EH的数量关系是.CG和EH的数量关系是,因此![]() = .
= .
(2)类比延伸:
在原题的条件下,若把“AF:EF=4:1”改为“AF:EF=n:1”(n>0),求![]() 的值.(用含有n的式子表示)
的值.(用含有n的式子表示)
(3)拓展迁移:
如图2,在四边形ABCD中,CD∥AB,点E是BC的延长线上的一点,AE与BD相交于点F.若AB:CD=a:1(a>0),BC:BE=b:1(b>0),则![]() = .(直接用含有a、b的式子表示,不写解答过程)
= .(直接用含有a、b的式子表示,不写解答过程)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某车库出口安装的栏杆如图所示,点A是栏杆转动的支点,点E是栏杆两段的联结点.当车辆经过时,栏杆AEF最多只能升起到如图2所示的位置,其示意图如图3所示(栏杆宽度忽略不计),其中AB⊥BC,EF∥BC,∠AEF=143°,AB=1.18米,AE=1.2米,那么适合该地下车库的车辆限高标志牌为( )(参考数据:sin37°≈0.60,cos37°≈0.80,tan37°≈0.75)
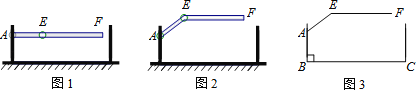
A. B.
B. C.
C. D.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,并完成相应的任务.
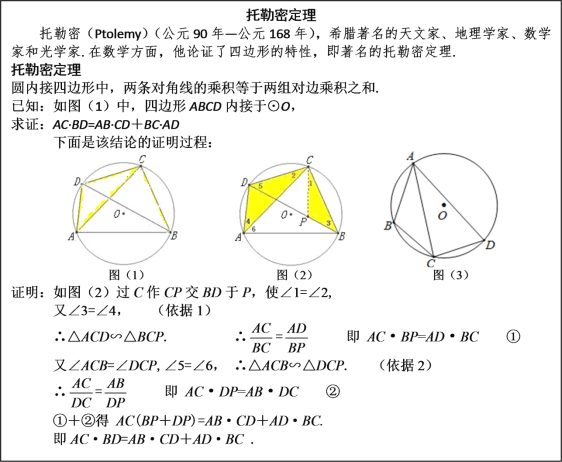
任务:
(1)上述证明过程中的“依据1”和“依据2”分别指什么?
依据1:
依据2:
(2)当圆内接四边形ABCD是矩形时,托勒密定理就是我们非常熟知的一个定理: (请写出定理名称).
(3)如图(3),四边形ABCD内接于⊙O,AB=3,AD=5,∠BAD=60°,点C是弧BD的中点,求AC的长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com