
【题目】如图,抛物线y=﹣x2+bx+c与x轴交于A(﹣1,0),B(5,0)两点,直线y=﹣![]() x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交 线段CD于点E,设点P的横坐标为m.
x+3与y轴交于点C,与x轴交于点D.点P是直线CD上方的抛物线上一动点,过点P作PF⊥x轴于点F,交 线段CD于点E,设点P的横坐标为m.
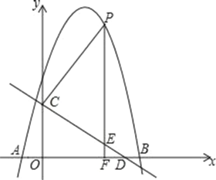
(1)求抛物线的解析式;
(2)求PE的长最大时m的值.
(3)Q是平面直角坐标系内一点,在(2)的情况下,以P、Q、C、D为顶点的四边形是平行四边形是否存在?若存在,请直接写出存在 个满足题意的点.
【答案】(1)![]() (2)当
(2)当![]() 时,
时,![]() 的长最大(3)
的长最大(3)![]()
【解析】
(1)根据待定系数法求解即可;
(2)设点![]() 的坐标为
的坐标为![]() 、点
、点![]() 的坐标为
的坐标为![]() ,列出
,列出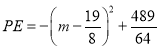 ,根据二次函数的图象性质求解即可;
,根据二次函数的图象性质求解即可;
(3)分以![]() 为对角线时、以
为对角线时、以![]() 为对角线时、以
为对角线时、以![]() 为对角线时三种情况进行讨论求解即可.
为对角线时三种情况进行讨论求解即可.
解:(1)∵抛物线![]() 与
与![]() 轴交于
轴交于![]() 、
、![]() 两点
两点
∴将![]() 、
、![]() 两点代入
两点代入![]() ,得:
,得:![]()
∴![]()
∴抛物线的解析式为:![]() .
.
(2)∵直线![]() 与
与![]() 轴交于点
轴交于点![]() ,与
,与![]() 轴交于点
轴交于点![]()
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴![]()
∵点![]() 的横坐标为
的横坐标为![]()
∴点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴
∵![]() ,
,![]()
∴当![]() 时,
时,![]() 的长最大.
的长最大.
(3)∵由(2)可知,点![]() 的坐标为:
的坐标为:![]()
∴以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形分为三种情况,如图:
为顶点的四边形是平行四边形分为三种情况,如图:
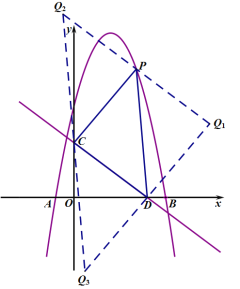
①以![]() 为对角线时
为对角线时
∵点![]() 的坐标为:
的坐标为:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴点![]() 的坐标为
的坐标为![]() ,即
,即![]() ;
;
②以![]() 为对角线时
为对角线时
∵点![]() 的坐标为:
的坐标为:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴点![]() 的坐标为
的坐标为![]() ,即
,即![]() ;
;
③以![]() 为对角线时
为对角线时
∵点![]() 的坐标为:
的坐标为:![]() ,点
,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]()
∴点![]() 的坐标为
的坐标为![]() ,即
,即![]() .
.
∴综上所述,在(2)的情况下,存在以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是平行四边形,点
为顶点的四边形是平行四边形,点![]() 的坐标为:
的坐标为:![]() 、
、![]() 或
或![]()
∴存在![]() 个满足题意的点.
个满足题意的点.


科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,AB=2,M为CD的中点,N为BC的中点,连接AM和DN交于点E,连接BE,作AH⊥BE于点H,延长AH与DN交于点F.连接BF并延长与CD交于点G,则MG的长度为__________.
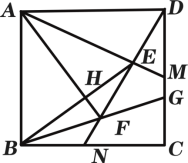
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某班“数学兴趣小组”对函数y=![]() ,的图象和性质进行了探究探究过程如下,请补充完成:
,的图象和性质进行了探究探究过程如下,请补充完成:
(1)函数y=![]() 的自变量x的取值范围是 ;
的自变量x的取值范围是 ;
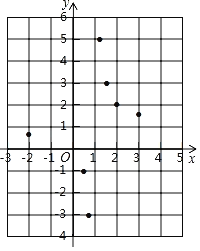
(2)下表是y与x的几组对应值.请直接写出m,n的值:m= ;n= .
x | … | ﹣2 | ﹣1 | 0 |
|
|
| n | 2 | 3 | 4 | … |
y | … |
| m | 0 | ﹣1 | ﹣3 | 5 | 3 | 2 |
|
| … |
(3)如图,在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(4)通过观察函数的图象,小明发现该函数图象与反比例函数y=![]() (k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,
(k>0)的图象形状相同,是中心对称图形,且点(﹣1,m)和(3,![]() )是一组对称点,则其对称中心的坐标为 .
)是一组对称点,则其对称中心的坐标为 .
(5)当2≤x≤4时,关于x的方程kx+![]() =
=![]() 有实数解,求k的取值范围.
有实数解,求k的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】美丽的黄河宛如一条玉带穿城而过,沿河两岸的滨河路风情线是兰州最美的景观之一.数学课外实践活动中,小林在南滨河路上的A,B两点处,利用测角仪分别对北岸的一观景亭D进行了测量.如图,测得∠DAC=45°,∠DBC=65°.若AB=132米,求观景亭D到南滨河路AC的距离(结果精确到1米,参考数据:sin65°≈0.91,cos65°≈0.42,tan65°≈2.14).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】今年疫情防控期间.某小区卫生所决定购买A,B两种口罩.以满足小区居民的需要.若购买A种口罩9包,B种口罩4包,则需要700元;若购买A种口罩3包.B种口罩5包.则需要380元.
(1)购买人A,B两种口罩每包各需名少元?
(2)卫生所准备购进这两种口罩共90包,并且A种口罩包数不少于B种口罩包数的2倍,请设计出最省钱的购买方案,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
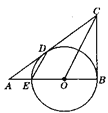
【题目】如图1,CB、CD是⊙O的切线,切点分别为B、D,CD的延长线与⊙O的直径BE的延长线交于A点,连OC,ED.
(1)探索OC与ED的位置关系,并加以证明;
(2)若OD=4,CD=6,求tan∠ADE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知:如图,在菱形ABCD 中,点E,O,F分别是边AB,AC,AD的中点,连接CE、CF、OE、OF.
(1)求证:△BCE≌△DCF;
(2)当AB与BC满足什么条件时,四边形AEOF正方形?请说明理由.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com