
 优百分课时互动系列答案
优百分课时互动系列答案科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源:黄冈难点课课练 八年级数学上册 题型:044
2002年8月,在北京召开国际数学大会,大会会标是由4个相同的直角三角形与一个小正方形拼成的大正方形,如图,若大正方形的面积为136,小正方形的面积为16
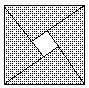
(1)判断直角三角形斜边是有理数还是无理数,并求出它介于哪两个整数之间?
(2)设l为直角三角形的周长,且m<l<n,其中m、n为正整数,求m+n的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
 ,四边形
,四边形 、
、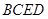 、
、 都是正方形.
都是正方形.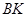 、
、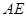 得到图2,则△
得到图2,则△ ≌△
≌△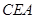 ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是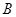 作
作 ⊥
⊥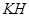 于
于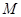 ,交
,交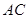 于
于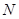 ,则
,则 △
△ ;同理
;同理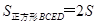 △
△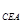 ,得
,得 ,然后可证得勾股定理.
,然后可证得勾股定理.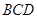 、△
、△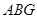 、△
、△ 的面积关系是 ▲ .
的面积关系是 ▲ .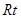 △
△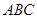 也进行“退化”为锐角△
也进行“退化”为锐角△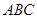 ,并擦去正方形
,并擦去正方形 得图4,由
得图4,由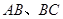 两边向三角形外作正△
两边向三角形外作正△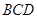 、正△
、正△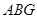 ,△
,△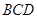 的外接圆与
的外接圆与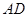 交于点
交于点 ,此时
,此时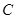 、
、 、
、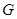 共线,从△
共线,从△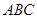 内一点到
内一点到 、
、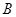 、
、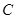 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点 (已经被他人证明).设
(已经被他人证明).设 =3,
=3,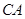 =4,
=4, .求
.求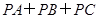 的值.
的值.
查看答案和解析>>
科目:初中数学 来源:2012届浙江省天台、椒江、玉环九年级第一次模拟考试数学卷(解析版) 题型:解答题
(14分)在研究勾股定理时,同学们都见到过图1,∠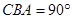 ,四边形
,四边形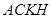 、
、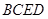 、
、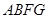 都是正方形.
都是正方形.
⑴连结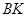 、
、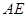 得到图2,则△
得到图2,则△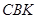 ≌△
≌△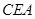 ,此时两个三角形全等的判定依据是
,此时两个三角形全等的判定依据是
▲ ;过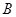 作
作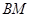 ⊥
⊥ 于
于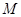 ,交
,交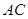 于
于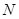 ,则
,则 △
△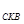 ;同理
;同理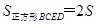 △
△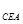 ,得
,得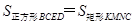 ,然后可证得勾股定理.
,然后可证得勾股定理.
⑵在图1中,若将三个正方形“退化”为正三角形,得到图3,同学们可以探究△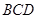 、△
、△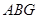 、△
、△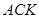 的面积关系是 ▲ .
的面积关系是 ▲ .
⑶为了研究问题的需要,将图1中的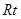 △
△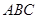 也进行“退化”为锐角△
也进行“退化”为锐角△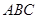 ,并擦去正方形
,并擦去正方形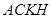 得图4,由
得图4,由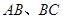 两边向三角形外作正△
两边向三角形外作正△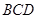 、正△
、正△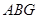 ,△
,△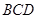 的外接圆与
的外接圆与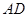 交于点
交于点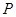 ,此时
,此时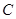 、
、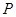 、
、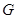 共线,从△
共线,从△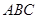 内一点到
内一点到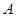 、
、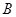 、
、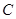 三个顶点的距离之和最小的点恰为点
三个顶点的距离之和最小的点恰为点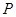 (已经被他人证明).设
(已经被他人证明).设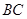 =3,
=3,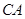 =4,
=4,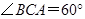 .求
.求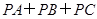 的值.
的值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com