
【题目】如图,正方形ABCD是一块绿化带,阴影部分EOFB,GHMN都是正方形的花圃,其中EOFB的顶点O是正方形中心.已知自由飞翔的小鸟,将随机落在这块绿化带上,则小鸟落在花圃上的概率为( )

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】C
【解析】设正方形ABCD的边长为a,根据正方形的性质∠ACB=∠ACD=45°,AC=![]() a,再利用四边形BEOF为正方形易得CF=OF=BF=
a,再利用四边形BEOF为正方形易得CF=OF=BF=![]() a,则S正方形BEOF=
a,则S正方形BEOF=![]() a2,设正方形MNGH的边长为x,易得CM=AN=MN=x,即3x=
a2,设正方形MNGH的边长为x,易得CM=AN=MN=x,即3x=![]() a,解得x=
a,解得x=![]() a,则S正方形MNGH=
a,则S正方形MNGH=![]() a2,然后根据几何概率的意义,用两个小正方形的面积和除以正方形ABCD的面积即可得到小鸟落在花圃上的概率,从而得到小鸟不落在花圃上的概率.
a2,然后根据几何概率的意义,用两个小正方形的面积和除以正方形ABCD的面积即可得到小鸟落在花圃上的概率,从而得到小鸟不落在花圃上的概率.
设正方形ABCD的边长为a,
∵四边形ABCD为正方形,
∴∠ACB=∠ACD=45°,AC=![]() a,
a,
∵四边形BEOF为正方形,
∴CF=OF=BF,
∴S正方形BEOF=(![]() a)2=
a)2=![]() a2,
a2,
设正方形MNGH的边长为x,
∵△ANG和△CMH都是等腰直角三角形,
∴CM=AN=MN=x,
∴3x=![]() a,解得x=
a,解得x=![]() a,
a,
∴S正方形MNGH=(![]() a)2=
a)2=![]() a2,
a2,
∴小鸟不落在花圃上的概率=(![]() a2+
a2+![]() a2 )÷a2=
a2 )÷a2=![]() .
.
故选C.


科目:初中数学 来源: 题型:
【题目】有一种节能型轿车的油箱加满天然气后,油箱中的剩余天然气量![]() (升)与轿车行驶路程
(升)与轿车行驶路程![]() (千米)之间的关系如图所示,根据图象回答下列问题:
(千米)之间的关系如图所示,根据图象回答下列问题:
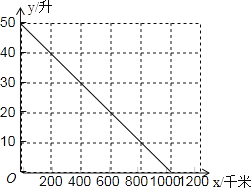
(1)这种轿车的油箱最多能装______升天然气,加满天然气后可供轿车行驶______千米.
(2)轿车每行驶200千米消耗天然气________升.
(3)写出![]() 与
与![]() 之间的函数关系式.
之间的函数关系式.
查看答案和解析>>
科目:初中数学 来源: 题型:
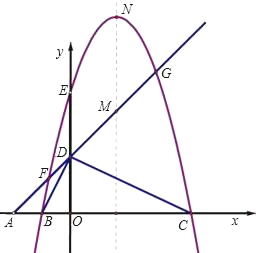
【题目】如图,平面直角坐标系中,点A、B、C在x轴上,点D、E在y轴上,OA=OD=2,OC=OE=4,B为线段OA的中点,直线AD与经过B、E、C三点的抛物线交于F、G两点,与其对称轴交于M,点P为线段FG上一个动点(与F、G不重合),PQ∥y轴与抛物线交于点Q.
(1)求经过B、E、C三点的抛物线的解析式;
(2)判断△BDC的形状,并给出证明;当P在什么位置时,以P、O、C为顶点的三角形是等腰三角形,并求出此时点P的坐标;
(3)若抛物线的顶点为N,连接QN,探究四边形PMNQ的形状:①能否成为菱形;②能否成为等腰梯形?若能,请直接写出点P的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】数轴是初中数学的一个重要工具,利用数轴可以将数与形完美地结合,研究数轴我们发现:若数轴上点A、点B表示的数分别为a、b,则A,B两点之间的距离AB=|a﹣b|,线段AB的中点表示的数为![]() .如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为
.如:如图,数轴上点A表示的数为﹣2,点B表示的数为8,则A、两点间的距离AB=|﹣2﹣8|=10,线段AB的中点C表示的数为![]() =3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
=3,点P从点A出发,以每秒3个单位长度的速度沿数轴向右匀速运动,同时点Q从点B出发,以每秒2个单位长度的速度向左匀速运动.设运动时间为t秒(t>0).
(1)用含t的代数式表示:t秒后,点P表示的数为 ,点Q表示的数为 .
(2)求当t为何值时,P、Q两点相遇,并写出相遇点所表示的数;
(3)求当t为何值时,PQ=![]() AB;
AB;
(4)若点M为PA的中点,点N为PB的中点,点P在运动过程中,线段MN的长度是否发生变化?若变化,请说明理由;若不变,请求出线段MN的长.
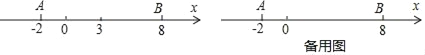
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知数轴上两点A、B对应的数分别是 6,﹣8,M、N、P为数轴上三个动点,点M从A点出发速度为每秒2个单位,点N从点B出发速度为M点的3倍,点P从原点出发速度为每秒1个单位.
(1)若点M向右运动,同时点N向左运动,求多长时间点M与点N相距54个单位?
(2)若点M、N、P同时都向右运动,求多长时间点P到点M,N的距离相等?
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
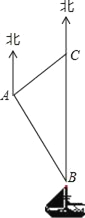
【题目】钓鱼岛是我国固有领土,现在我边海渔民要在钓鱼岛附近进行捕鱼作业,当渔船航行至B处时,测得该岛位于正北方向20(1+![]() )海里的C处,为了防止某国海警干扰,请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向,A位于B的北偏西30°方向,求A、C之间的距离.
)海里的C处,为了防止某国海警干扰,请求我A处的鱼监船前往C处护航,已知C位于A处的北偏东45°方向,A位于B的北偏西30°方向,求A、C之间的距离.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解不等式组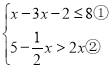 并求其整数解的和.
并求其整数解的和.
解:解不等式①,得_______;
解不等式②,得________;
把不等式①和②的解集在数轴上表示出来:
![]()
![]() 原不等式组的解集为________,
原不等式组的解集为________,
由数轴知其整数解为________,和为________.
在解答此题的过程中我们借助于数轴上,很直观地找出了原不等式组的解集及其整数解,这就是“数形结合的思想”,同学们要善于用数形结合的思想去解决问题.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为测量一座山峰CF的高度,将此山的某侧山坡划分为AB和BC两段,每一段山坡近似是“直”的,测得坡长AB=800米,BC=200米,斜坡AB的坡度![]() ,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2,
,仰角∠CBE=50°.则山峰的高度CF约为( )米.(可用的参考数据:sin50°≈0.8,tan50°≈1.2, ![]() )
)
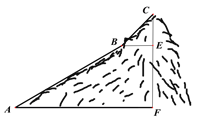
A. 500 B. 518 C. 530 D. 580
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某中学为了科学建设“学生健康成长工程”.随机抽取了部分学生家庭对其家长进行了主题为“周末孩子在家您关心吗?”的问卷调查,将回收的问卷进行分析整理,得到了如下的样本统计表和扇形统计图:
代号 | 情况分类 | 家庭数 |
| 带孩子玩并且关心其作业完成情况 | 16 |
| 只关心其作业完成情况 | b |
| 只带孩子玩 | 8 |
| 既不带孩子玩也不关心其作业完成情况 | d |
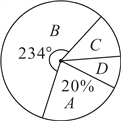
(1)求![]() 的值;
的值;
(2)该校学生家庭总数为500,学校决定按比例在![]() 类家庭中抽取家长组成培训班,其比例为
类家庭中抽取家长组成培训班,其比例为![]() 类取20%,
类取20%,![]() 类各取60%,请你估计该培训班的家庭数;
类各取60%,请你估计该培训班的家庭数;
(3)若在![]() 类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在
类家庭中只有一个城镇家庭,其余是农村家庭,请用列举法求出在![]() 类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
类中随机抽出2个家庭进行深度采访,其中有一个是城镇家庭的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com