练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    【题目】已知直线：与直线：交于点（2，4），直线与轴交于点，直线与轴交于点.

    （1）求，的值；

    （2）求当为何值时，，；

    （3）求△的面积.

    【答案】(1)m=4,n=6;(2)x>2时，；x<2时，； (3)5.

    【解析】

    （1）根据点（2，4）在直线：与直线：的函数图象上，求出，的值；

    （2）根据（1）求出函数解析式，要求，则解不等式即可；

    （3）分别求出B、C两点的坐标然后求三角形面积即可.

    解：（1）根据点（2，4）在直线：与直线：的函数图象上

    ∴，

    ∴m=4，n=6；

    （2）根据（1）知，

    ∴要使即

    要使即

    ；

    （3）根据直线与轴交于点，直线与轴交于点

    ∴当时x=1，即点的坐标为（1，0），

    当时，即点C的坐标为（0，6）

    当时，即点D的坐标为（0，-4）

    如下图

    ∴

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：

    【题目】某市举行“传承好家风”征文比赛，已知每篇参赛征文成绩记m分（60≤m≤100），组委会从1000篇征文中随机抽取了部分参赛征文，统计了它们的成绩，并绘制了如图不完整的两幅统计图表．

    征文比赛成绩频数分布表

    分数段

    频数

    频率

    60≤m＜70

    38

    0.38

    70≤m＜80

    a

    0.32

    80≤m＜90

    b

    c

    90≤m≤100

    10

    0.1

    合计

    1

    请根据以上信息，解决下列问题：

    （1）征文比赛成绩频数分布表中c的值是_____；

    （2）补全征文比赛成绩频数分布直方图；

    （3）若80分以上（含80分）的征文将被评为一等奖，试估计全市获得一等奖征文的篇数．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，某计算机中有、、三个按键，以下是这三个按键的功能．

    (1)．：将荧幕显示的数变成它的正平方根，例如：荧幕显示的数为49时，按下后会变成7．

    (2)．：将荧幕显示的数变成它的倒数，例如：荧幕显示的数为25时，按下后会变成0.04．

    (3)．：将荧幕显示的数变成它的平方，例如：荧幕显示的数为6时，按下后会变成36．

    若荧幕显示的数为100时，小刘第一下按，第二下按，第三下按，之后以、、的顺序轮流按，则当他按了第100下后荧幕显示的数是多少（　　）

    A. 0.01 B. 0.1 C. 10 D. 100

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在长方形ABCD中，点E是AD的中点，连接CE，将△CDE沿着CE翻折得到△CFE，EF交BC于点G，CF的延长线交AB的延长线于点H，若AH＝25，BC＝40，则FG＝_____．

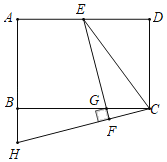
    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，在平面直角坐标系中，直线l1：y＝与x轴、y轴分别相交于点A、B，直线l2与直线y＝﹣x平行，且与直线l1相交于点B，与x轴交于点C．

    （1）求点C坐标；

    （2）若点P是y轴右侧直线l1上一动点，点Q是直线l2上一动点，点D（﹣2，6），求当S△PBC＝S四边形AOBD时，点P的坐标，并求出此时，PQ+DQ的最小值；

    （3）将△AOB沿着直线l2平移，平移后记为△A1O1B1，直线O1B1交11于点M，直线A1B1交x轴于点N，当△B1MN是等腰三角形时，求点A1的横坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，将一根长为的牙刷放置在底面直径为、高为的圆柱形牙刷筒中，则牙刷露在筒外的长度最小为（ ）

    A.B.C.D.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】在学习《实数》内容时，我们估算带有根号的无理数的近似值时，经常使用“逐步逼近”的方法来实现的.“逐步逼近”是数学思维方法的一种重要形式，主要通过构造“拟对象”、逐步扩充元素、逐步扩充范围、放缩逼近、合力逼近等方式解决问题.

    例如：估算的近似值时，利用“逐步逼近”法可以得出.请你根据阅读内容回答下列问题：

    （1）介于连续的两个整数和，且，那么______，______；

    （2）的整数部分是______，小数部分是______；

    （3）已知的小数部分为，的小数部分为，求的值.

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】如图，菱形中，对角线，相交于点，且，，动点，分别从点，同时出发，运动速度均为，点沿运动，到点停止，点沿运动，到点停止后继续运动，到点停止，连接，，．设的面积为（这里规定：线段是面积的几何图形），点的运动时间为．

    填空：________，与之间的距离为________；

    当时，求与之间的函数解析式；

    直接写出在整个运动过程中，使与菱形一边平行的所有的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：

    【题目】某校想知道学生对宜宾着力打造生态城市，三江六岸投入300多亿元实施长江生态综合治理工程的了解程度，在该校随机抽取了部分学生进行问卷，问卷有以下四个选项：:十分了解；:了解较多；:了解较少；:不了解（要求：每名被调查的学生必选且只能选择一项），现将调查的结果绘制成两幅不完整的统计图．请根据两幅统计图中的信息回答下列问题．

    （1）在被调查的人中，“了解较多”的人数是 人；

    （2）扇形统计图中的选项“了解较少”部分所占扇形的圆心角的大小为 ；

    （3）若该校共有2000名学生，请你根据上述调查结果，估计该校学生对宜宾着力打造生态城市，三江六岸投入300多亿元实施长江生态综合治理工程的了解程度“十分了解”和“了解较多”的学生共有多少名？

    查看答案和解析>>

    同步练习册答案