
在△ABC中,∠A=90°,BC=10,tan∠ABC=3:4,M是AB上的动点(不与A,B重合),过M点作MN∥BC交AC于点N,以AM、AN为邻边作矩形AMPN,其对角线交点为G。直线MP、NP分别与边BC相交于点E、F,设AP=x。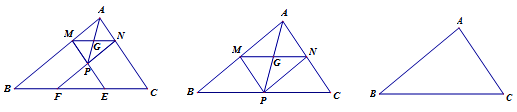
图1 图2
(1)求AB、AC的长;
(2)如图2,当点P落在BC上时,求x的值;
(3)当EF=5时,求x的值;
(4)在动点M的运动过程中,记△MNP与梯形BCNM重合部分的面积为y。试求y关于x的函数表达式,并求出y的最大值。
(1)AB="8,AC=6;" (2) x=5;(3)x=2.5或7.5 (4)当0<x≤5时, ;
;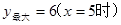 ;当5<x<10时,
;当5<x<10时,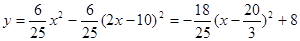 ;
;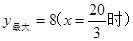
解析试题分析:(1)在△ABC中,∠A=90°,BC=10,tan∠ABC=3:4,而根据三角函数tan∠ABC= ,令AC=3K;AB=4K;)在△ABC中由勾股定理解得K=2;所以AB=8,AC=6;
,令AC=3K;AB=4K;)在△ABC中由勾股定理解得K=2;所以AB=8,AC=6;
(2) 在△ABC中,∠A=90°,当点P落在BC上时以AM、AN为邻边作矩形AMPN,那么点P是BC的中点,所以AP是直角三角形斜边上的中线,等于斜边的一半,所以x=5;
(3) 当EF=5时;根据题意BF=CE=2.5;∵MN//BC,NF//AB,ME//AC ∴四边形BFNM和四边形CEMN都是平行四边形(两组对边分别平行的四边形是平行四边形),∴MN=BF;矩形AMPN,所以AP=MN=2.5;同理解得AP=7.5;所以x=2.5或7.5;
(4)当0<x≤5时, ;
;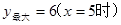
当5<x<10时,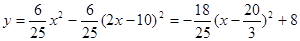 ;
;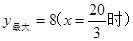
故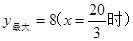
考点:三角形及四边形
点评:本题主要考查平行四边形的判定方法和性质,矩形的性质,对它们的熟练掌握是解本题的关键


科目:初中数学 来源: 题型:
 23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
23、如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
 18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于
18、如图,在△ABC中,边AC的垂直平分线交BC于点D,交AC于点E、已知△ABC中与△ABD的周长分别为18cm和12cm,则线段AE的长等于查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com