
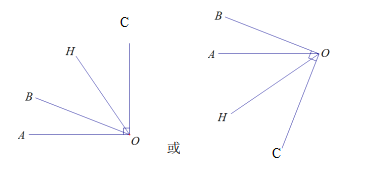
����Ŀ���Ķ��������:С����������һ������: ��ͼ1��![]() ���뻭һ��
���뻭һ��![]() ��ʹ
��ʹ![]() ��
��![]() ����.
����.

С��������˼����:����ͨ��������ȷ����![]() ��
��![]() ���ⲿ������ʾ��ͼ����ͼ2��ʾ:Ȼ��ͨ������ƽ���ҵ�
���ⲿ������ʾ��ͼ����ͼ2��ʾ:Ȼ��ͨ������ƽ���ҵ�![]() �IJ���
�IJ���![]() ��
��

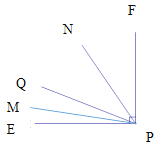
��ͼ3��ʾ:��������Ҫʹ![]() ��
��![]() ����������
����������![]() .
.

��ˣ�С���ҵ��˽������ķ���:�����ӳ�����![]() �õ�����
�õ�����![]() ����������������
����������������![]() ��ƽ����
��ƽ����![]() �������͵õ���
�������͵õ���![]() ��
��![]() ����
����
(1)С�ϸ����Լ��Ļ���д���˼�֪����֤���������֤��.��֪:��ͼ3����![]() ��ֱ��
��ֱ��![]() �ϣ�����
�ϣ�����![]() ƽ��
ƽ��![]() .��֤:
.��֤: ![]() ��
��![]() ����. .
����. .

(2)�ο�С�ϵĻ�����������ͼ�л���--��![]() ��ʹ
��ʹ![]() ��
��![]() ����.(������ͼ�ۼ�)
����.(������ͼ�ۼ�)

(3)��֪![]() ��
��![]() ���࣬����
���࣬����![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]() .��
.��![]() ��ֱ��д�����
��ֱ��д�����![]() �Ķ����� .
�Ķ����� .
���𰸡���1������������2������������3��![]() ��
��![]()
��������
(1)�����ڲ��ǵĶ���ó�![]() ���ٸ��ݽ�ƽ���ߵĶ���ɵ�
���ٸ��ݽ�ƽ���ߵĶ���ɵ�![]() ���Ӷ��ó�
���Ӷ��ó�![]() ��
��![]() ����.
����.
(2)�ȹ���ֱ�ǣ���![]() ��
��![]() ������������������
������������������![]() ��
��![]() ��ƽ����
��ƽ����![]() �����ɵó�
�����ɵó�![]() ��
��![]() ����
����
(3)�ȷ�PF��PQ���Ҳ����࣬����ͼ�Σ��ٸ��ݽ�ƽ���ߵ����ʺͽǵĺͲ�ɵó�����
�⣺(1)֤��:![]() ��
��![]() ��ֱ��
��ֱ��![]() �ϣ�
�ϣ�
![]() .
.
��![]() .
.
![]() .
.
![]() ƽ��
ƽ��![]() ��
��
![]() .
.
![]()
![]() ��
��![]() ����.
����.
(2) ��![]() ��
��![]() ���ٷֱ�
���ٷֱ�![]() ��
��![]() ��ƽ����
��ƽ����![]()
��ͼ��ʾ
(3) ��PF��PQ���Ҳ�ʱ���������⻭��ͼ����ͼ
������![]() ƽ��
ƽ��![]() ������
������![]() ƽ��
ƽ��![]() .
.
��![]() ��
��![]()
��![]()
��![]() ��
��![]() ���࣬
���࣬
��![]()
��![]()
��PF��PQ���Ҳ�ʱ���������⻭��ͼ��
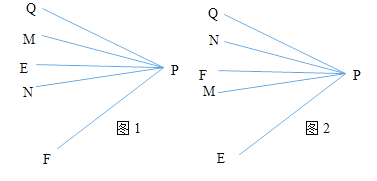
��ͼ1��������PMƽ��![]() ������
������![]() ƽ��
ƽ��![]() .
.
��![]() ��
��![]()
��![]()
��![]() ��
��![]() ���࣬
���࣬![]()
��![]()
��![]()
��ͼ2��PMƽ��![]() ������
������![]() ƽ��
ƽ��![]() .
.
��![]() ��
��![]()
��![]()
��![]() ��
��![]() ���࣬
���࣬![]()
��![]()
��![]()
���������ɵã�![]() =45����
=45����![]()
�ʴ�Ϊ��45����![]()



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ��E��F�ֱ�Ϊ����ABCD�ı�AD��BC�ϵĵ㣬AE=CF����֤��BE=DF��

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����ҹ�ʵʩ�����������𣬿�ʼ�г�ʹ�û����������Ϊ�������г�����ij��������A��B���ֿ�ʽ�IJ��ʻ����������ÿ������4500�������ֹ�����ijɱ����ۼ����±�������ÿ������A�ֹ���� x����
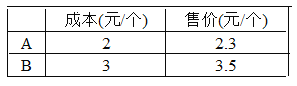
��1���ú�x����ʽ��ʾÿ��������ɱ��������л���
��2���ú�x����ʽ��ʾÿ���õ��������л���(�����ۼۣ��ɱ�)��
��3����x��1500ʱ����ÿ��������ɱ���ÿ���õ�����
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij�̳�����һ�ֵ���Ϊ40Ԫ�����������Ե���50Ԫ���ۣ���ôÿ�¿��۳�30�����������۾��飬�ۼ�ÿ���5Ԫ����������Ӧ����1����
��1����д���ܵ���������yԪ�����۵������xԪ֮��ĺ�����ϵʽ��
��2��������Ǿ�����Ϊʹÿ�µ��������������ô��ȷ����������ĵ���Ϊ����Ԫ����ʱ����������Ƕ���Ԫ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�����㣺
(1)12��(��18)��(��5)��6��
(2)12��(��![]() )��8��
)��8��
(3)2��2��(��![]() ����3��
����3��
(4)��12��![]() ������2)3�� (��3)2��
������2)3�� (��3)2��
(5)(��![]() ��
��![]() ��
��![]() )��(��60)��
)��(��60)��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������е���1���ߣ�������վ����������Ժվ������11����վ��2019��4��1����ʽ��ͨ��Ӫ����־�ż�������ʽ����������ʱ������11��վ����ͼ��ʾ��

ij�죬����������վ��ʼ�����������ڵ�����վ����־���߷���Aվ�³�ʱ������־���߷���������Լ������Ժվ����Ϊ��������ij˳���¼���£���λ��վ������3����2����6����7����5����3��+6��
(1)��ͨ������˵��Aվ����һվ?
(2)��������վ֮��ľ���Ϊ3ǧ�ף����������־�շ����ڼ���������н���·���Ƕ���ǧ��?
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����ƽ��ֱ������ϵ�У���A��0��4����B��3��0��������AB������AOB�ع���B��ֱ���۵���ʹ��A����x���ϵĵ�A�������ۺ����ڵ�ֱ�߽�y���������ڵ�C����ֱ��BC�Ľ���ʽΪ�� ����
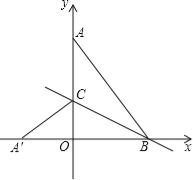
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ�������ڱ߷ֱ���ȵ��ı��ν��������Ρ�����ͼ���ı���![]() ��һ�����Σ�����
��һ�����Σ�����![]() ��
��![]() ���õ����½��ۣ���
���õ����½��ۣ���![]() ����
����![]() ����
����![]() .��
.��![]() ƽ��
ƽ��![]() ��
��![]() ����
����![]() ��
��![]() ����ƽ�֣�������ȷ�Ľ����У�����ţ�________.
����ƽ�֣�������ȷ�Ľ����У�����ţ�________.

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����2016������ʡ�������У���֪����ABC�ڽ��ڡ�O��D��![]() ��һ�㣬OD��BC������ΪH��
��һ�㣬OD��BC������ΪH��
��1����ͼ1����Բ��O��AB����ʱ����֤��AC=2OH��
��2����ͼ2����Բ��O����ABC�ⲿʱ������AD��CD��AD��BC���ڵ�P����֤����ACD=��APB��
��3���ڣ�2���������£���ͼ3������BD��EΪ��O��һ�㣬����DE��BC�ڵ�Q����AB�ڵ�N������OE��BFΪ��O���ң�BF��OE�ڵ�R��DE�ڵ�G������ACD����ABD=2��BDN��AC=![]() ��BN=
��BN=![]() ��tan��ABC=
��tan��ABC=![]() ����BF�ij���
����BF�ij���

�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com