
【题目】如图,已知直线![]() 与
与![]() 轴、
轴、![]() 轴分别交于
轴分别交于![]() 、
、![]() 两点,
两点,![]() 是以
是以![]() 为圆心,1为半径的圆上一动点,连接
为圆心,1为半径的圆上一动点,连接![]() 、
、![]() ,当
,当![]() 的面积最大时,点
的面积最大时,点![]() 的坐标为_______.
的坐标为_______.
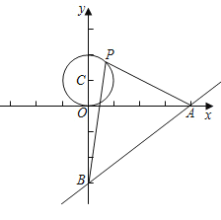
【答案】(![]() ,
,![]() )
)
【解析】
过C作CM⊥AB于M,交x轴于E,连接AC,MC的延长线交⊙C于D,作DN⊥x轴于N,则由三角形面积公式得,![]() ×AB×CM=
×AB×CM=![]() ×OA×BC,可知圆C上点到直线y=
×OA×BC,可知圆C上点到直线y=![]() x-3的最长距离是DM,当P点在D这个位置时,△PAB的面积最大,先证得△COE∽△CMB,求得OE、CE,再通过证得△COE∽△DNE,求得DN和NE,由此求得答案.
x-3的最长距离是DM,当P点在D这个位置时,△PAB的面积最大,先证得△COE∽△CMB,求得OE、CE,再通过证得△COE∽△DNE,求得DN和NE,由此求得答案.
过C作CM⊥AB于M,交x轴于E,连接AC,MC的延长线交⊙C于D,作DN⊥x轴于N,
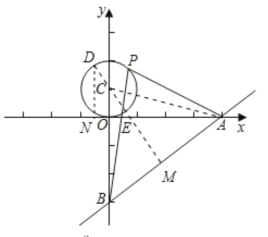
∵直线![]() 与x轴、y轴分别交于A,B两点,
与x轴、y轴分别交于A,B两点,
令x=0,得y=-3,
令y=9,得x=4
∴A(4,0),B(0,3),
∴OA=4,OB=3,
∴AB=![]()
则由三角形面积公式得,![]() ×AB×CM=
×AB×CM=![]() ×OA×BC,
×OA×BC,
∴![]() ×5×CM=
×5×CM=![]() ×4×(1+3),
×4×(1+3),
∴CM=![]()
∴BM=![]()
∴圆C上点到直线![]() 的最大距离是DM=1+
的最大距离是DM=1+![]() =
=![]()
当P点在D这个位置时,△PAB的面积最大,
∵∠CMB=∠COE=90°,∠OCE=∠MCB,
∴△COE∽△CMB,
∴![]()
∴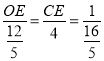
∴OE=,CE=![]() ,
,
∴ED=1+![]() =
=![]()
∵DN⊥x轴,
∴DN∥OC,
∴△COE∽△DNE,
∴![]() ,即
,即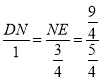
∴DN=![]() ,NE=
,NE=![]()
∴ON=NEOE=![]()
![]() =
=![]()
∴D(![]() ,
,![]() )
)
∴当△PAB的面积最大时,点P的坐标为(![]() ,
,![]() )
)
故答案为:(![]() ,
,![]() )
)


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】小明遇到这样一个问题:如图,矩形纸片ABCD,AB=2,BC=3,现要求将矩形纸片剪两刀后拼成一个与之面积相等的正方形,小明尝试给出了下面四种剪的方法,如图①②③④,图中BE=![]() .其中剪法正确的是( )
.其中剪法正确的是( )

A.①②B.①③C.②③D.③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在边长为1个单位长度的小正方形组成的网格中,给出了格点![]() (顶点是网格线的交点)和直线l及点O.
(顶点是网格线的交点)和直线l及点O.
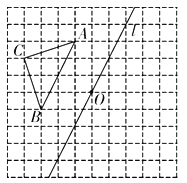
(1)画出![]() 关于直线l对称的
关于直线l对称的![]() ;
;
(2)连接OA,将OA绕点O顺时针旋转![]() ,画出旋转后的线段;
,画出旋转后的线段;
(3)在旋转过程中,当OA与![]() 有交点时,旋转角
有交点时,旋转角![]() 的取值范围为________.
的取值范围为________.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在半径为6的⊙O中,正六边形ABCDEF与正方形AGDH都内接于⊙O,则图中阴影部分的面积为( )
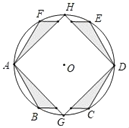
A. 27﹣9![]() B. 18
B. 18![]() C. 54﹣18
C. 54﹣18![]() D. 54
D. 54
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在菱形ABCD中,点E,F分别在AB,CD上,且![]() ,连接EF交BD于点O连接AO.若
,连接EF交BD于点O连接AO.若![]() ,,则
,,则![]() 的度数为( )
的度数为( )
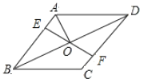
A.50°B.55°C.65°D.75°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,以![]() 的边
的边![]() 为直径作
为直径作![]() ,点
,点![]() 在
在![]() 上,
上,![]() 是
是![]() 的弦,
的弦,![]() ,过点
,过点![]() 作
作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() 交
交![]() 的延长线于点
的延长线于点![]() .
.
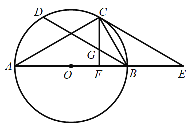
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)求证:![]() ;
;
(3)若![]() ,CG=4,求
,CG=4,求![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在矩形![]() 中,已知
中,已知![]() ,
,![]() ,点
,点![]() 是对角线
是对角线![]() 上一动点(不与
上一动点(不与![]() ,
,![]() 重合),连接
重合),连接![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 于点
于点![]() ,
,
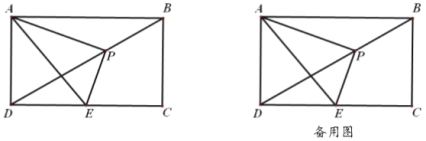
(1)求证:![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的值;
的值;
(3)在点![]() 运动过程中,当
运动过程中,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某家具生产厂生产某种配套桌椅(一张桌子,两把椅子),已知每块板材可制作桌子![]() 张或椅子
张或椅子![]() 把,现计划用
把,现计划用![]() 块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用
块这种板材生产一批桌椅(不考虑板材的损耗,恰好配套),设用![]() 块板材做椅子,用
块板材做椅子,用![]() 块板材做桌子,则下列方程组正确的是( )
块板材做桌子,则下列方程组正确的是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com