
已知:如图,AB、AC、ED分别切⊙O于点B、C、D,且AC⊥DE,垂足为E,BC的延长线交直线DE于点F,若BC=24,sin∠F=![]() .
.
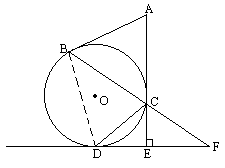
(1)求EF的长;
(2)试判断直线AB与CD是否平行,若平行,给出证明;若不平行,说明理由.
|
解:(1)∵AC⊥DE,∴∠CEF= ∵sin∠F= ∵ED、EC分别与⊙O相切, ∴ED=EC=3x. 由切割线定理知:FD2=FC·FB. ∴(7x2)=5x(5x+24). 化简整理,得x2-5x=0, ∴x1=5,x2=0(不合题意,舍去). ∴EF=4x=20. (2)AB与CD不平行,下面证明之. [证法一] 连结BD.∵ED切⊙O于点D, ∴∠CBD=∠CDF, 又∵∠F=∠F, ∴△BDF∽△DCF. ∴ 由(1)知CF=5x=25,DF=7x=35, 在等腰直角△CDE中,由勾股定理得DC=15 把CF=25,DF=35,DC=15 在△BDC中,∵BD≠BC, ∴∠BDC≠∠BCD. 而∠ABC=∠BDC(弦切角定理), ∴∠ABC≠∠BCD, ∴AB与CD不平行. 此题还可以用反证法来证明.思路是:假定AB∥CD(否定结论),由此导致矛盾,故断言AB与CD不平行. [证法二] 假设AB∥CD,则∠BCD=∠ABC, 又∵∠BDC=∠ABC, ∴∠BCD=∠BDC,则BD=BC=24. 由△BDF∽△DCF,得 由(1)知CF=25,DF=35,在等腰直角三角形DCE中,可求得DC=15 ∴ ∴BD=21 ∴假设不成立. ∴AB与CD不平行. |
|
(1)本小题要求EF的长,需要找出它与已知线段BC的关系,求解的关键在于利用条件sin∠F= (2)本小题是个开放性问题,面对开放性问题的多种可能结论,往往是首先作出“猜想”,然后再给出严格证明或科学解释.本题只要根据条件准确地作出图形,就能观察出AB、CD是不平行的.而证明两直线不平行的主要依据是平行线性质定理的逆否定理,为此,连结BD,通过它来证明它们有一对内错角不相等. |


科目:初中数学 来源: 题型:
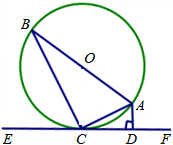 已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D.
已知:如图,AB是⊙O的直径,AC是弦,直线EF是过点C的⊙O的切线,AD⊥EF于点D. | AC |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com