矩形一条边上的中点与对边两个端点的连线互相垂直,已知矩形的周长为30cm,那么矩形的面积为________.
50cm
2分析:作出图形,根据点E是AB的中点,可得AE=DE,然后利用边角边定理证明△ABE与△DCE全等,根据全等三角形对应边相等可得BE=CE,又BE⊥CE,所以△BCE是等腰直角三角形,从而推出△ABE也是等腰直角三角形,得到矩形的长是宽的2本,根据周长是30cm分别求出长与宽,再利用面积公式计算即可求解.
解答:
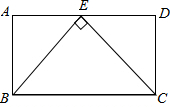
解:如图,∵E是AB的中点,
∴AE=DE,
∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=CD,
在△ABE与△DCE中,
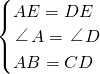
,
∴△ABE≌△DCE(SAS),
∴BE=CD,
∵BE⊥CE,
∴△BCE是等腰直角三角形,
∴∠CBE=45°,
∴∠ABE=90°-45°=45°,
∴△ABE也是等腰直角三角形,
∴AB=AE=

AD,
∴2(AB+AD)=30,
解得AB=5cm,AD=10cm,
∴矩形的面积为:AB•AD=5×10=50cm
2.
故答案为:50cm
2.
点评:本题考查了矩形的性质,全等三角形的判定与性质,矩形的周长与面积公式,证明出矩形的长是宽的2倍是解本题的关键.

 解:如图,∵E是AB的中点,
解:如图,∵E是AB的中点,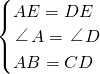 ,
, AD,
AD,

 同步练习河南大学出版社系列答案
同步练习河南大学出版社系列答案 同步练习西南大学出版社系列答案
同步练习西南大学出版社系列答案 补充习题江苏系列答案
补充习题江苏系列答案