
直线![]() 分别与
分别与![]() 轴、
轴、![]() 轴交于B、A两点.
轴交于B、A两点.
⑴求B、A两点的坐标;
⑵把△AOB以直线AB为轴翻折,点O落在平面上的点C处,以BC为一边作等边△BCD求D点的坐标.
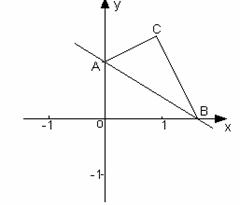
解:如图(1)令x=0,由![]() 得 y=1
得 y=1
令y=0,由![]() 得
得![]()
∴B点的坐标为(![]() ,0),A点的坐标为(0,1)
,0),A点的坐标为(0,1)
(2)由(1)知OB=![]() ,OA=1
,OA=1
∴tan∠OBA=![]() =
=![]() ∴∠OBA=30°
∴∠OBA=30°
∵△ABC和△ABO关于AB成轴对称
∴BC=BO=![]() ,∠CBA=∠OBA=30° ∴ ∠CBO=60°
,∠CBA=∠OBA=30° ∴ ∠CBO=60°
过点C作CM⊥x轴于M,则在Rt△BCM中
CM=BC×sin∠CBO=![]() ×sin60°=
×sin60°=![]()
BM=BC×cos∠CBO=![]() ×cos60°=
×cos60°=![]() ∴OM=OB-BM=
∴OM=OB-BM=![]() -
-![]() =
=![]()
∴C点坐标为(![]() ,
,![]() )
)
连结OC
∵OB=CB,∠CBO=60°
∴△BOC为等边三角形
过点C作CE∥x轴,并截取CE=BC则∠BCE=60°
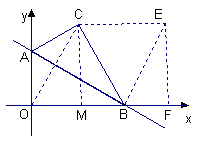 连结BE则△BCE为等边三角形.
连结BE则△BCE为等边三角形.
作EF⊥x轴于F,则EF= CM=![]() ,BF=BM=
,BF=BM=![]()
OF=OB+BF=![]() +
+![]() =
=![]()
∴点E坐标为(![]() ,
,![]() )
)
∴D点的坐标为(0,0)或(![]() ,
,![]() )
)


科目:初中数学 来源:2011-2012学年上海市松江初三二模数学试卷(解析版) 题型:解答题
已知直线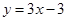 分别与
分别与 轴、
轴、 轴交于点
轴交于点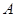 、
、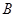 ,抛物线
,抛物线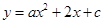 经过点
经过点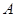 、
、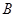 .
.
(1)求该抛物线的表达式,并写出该抛物线的对称轴和顶点坐标;
(2)记该抛物线的对称轴为直线 ,点
,点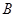 关于直线
关于直线 的对称点为
的对称点为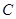 ,若点
,若点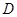 在
在 轴的正半轴上,且四边形
轴的正半轴上,且四边形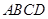 为梯形.
为梯形.
① 求点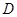 的坐标;
的坐标;
② 将此抛物线向右平移,平移后抛物线的顶点为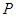 ,其对称轴与直线
,其对称轴与直线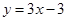 交于点
交于点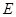 ,若tan
,若tan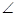
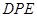 =
=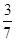 ,求四边形
,求四边形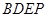 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源:2010-2011年山东肥城马埠中学初三模拟试题二数学卷 题型:选择题
已知:如图,直线 分别与
分别与 轴,
轴, 轴交于
轴交于 两点,从点
两点,从点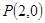 射出的光线经直线
射出的光线经直线 反射后再射到直线
反射后再射到直线 上,最后经直线
上,最后经直线 反射后又回到
反射后又回到 点,则光线所经过的路程是( )
点,则光线所经过的路程是( )
A.  B.
B.
 C.
C. D.
D. 

查看答案和解析>>
科目:初中数学 来源:2010--2011学年山东肥城马埠中一学初三月考数学试卷(二) 题型:选择题
已知:如图,直线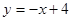 分别与
分别与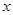 轴,
轴,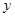 轴交于
轴交于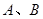 两点,从点
两点,从点 射出的光线经直线
射出的光线经直线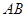 反射后再射到直线
反射后再射到直线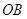 上,最后经直线
上,最后经直线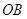 反射后又回到
反射后又回到 点,则光线所经过的路程是( )
点,则光线所经过的路程是( )
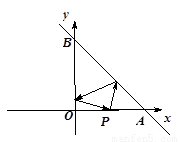
A. 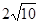 B.
B. 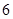 C.
C. D.
D. 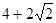
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com