
【题目】学着说点理:补全证明过程:
如图,![]() 于点
于点![]() ,若
,若![]() ,求
,求![]() 的度数。
的度数。
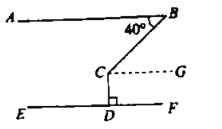
解:过点![]() 作
作![]() 。
。
![]() ,
,
![]() (________________)①
(________________)①
![]() ________。②(两直线平行,内错角相等)
________。②(两直线平行,内错角相等)
![]() ,
,
![]() 。(________________)③
。(________________)③
![]() ________________。④(等量代换)
________________。④(等量代换)
![]() ,
,
![]() 。(________________)⑤
。(________________)⑤
![]() ,
,
![]() 。
。
则![]() ________________ 。⑥
________________ 。⑥
【答案】平行于同一条直线的两条直线平行;EDC;垂直的定义;90°;两直线平行,内错角相等;130°.
【解析】
过点C作CG∥AB.依据平行线的性质,即可得到∠DCG=90°,∠BCG=40°,进而得到∠BCD的度数.
解:如图,过点C作CG∥AB.
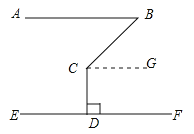
∵AB∥EF,
∴CG∥EF.(平行于同一条直线的两条直线平行)
∴∠GCD=∠EDC.(两直线平行,内错角相等)
∵CD⊥FF,
∴∠CDE=90°.(垂直的定义)
∴∠GCD=90°.(等量代换)
∵CG∥AB,
∴∠B=∠BCG.(两直线平行.内错角相等)
∵∠B=40°.
∴∠BCG=40°,
则∠BCD=∠BCG+∠GCD=130°.
故答案为:平行于同一条直线的两条直线平行;EDC;垂直的定义;90°;两直线平行,内错角相等;130°.


科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题:
利用完全平方公式![]() ,通过配方可对
,通过配方可对![]() 进行适当的变形,如
进行适当的变形,如![]() 或
或![]() ,从而使某些问题得到解决,
,从而使某些问题得到解决,
例:已知![]() ,
,![]() .求
.求![]() 的值.
的值.
解:![]() =19
=19
问题:已知:![]() ,求下列代数式的值.
,求下列代数式的值.
(1)![]() ;
;
(2)![]() .
.
(3)已知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形![]() 中,点
中,点![]() 到直线
到直线![]() ,
,![]() 的距离相等为
的距离相等为![]() ,
, ![]() ,
,![]() 平分
平分![]() ,
,![]() 长为n,且
长为n,且![]() ,四边形
,四边形![]() 的面积为6.
的面积为6.

(1)求线段![]() 的长;
的长;
(2)![]() 为
为![]() 延长线上一点,
延长线上一点,![]() ,交
,交![]() 延长线于
延长线于![]() ,探究
,探究![]() 、
、![]() 、
、![]() 的数量关系并说明理由;
的数量关系并说明理由;
(3)作![]() 平行
平行![]() 交
交![]() 延长线于
延长线于![]() ,
,![]() 平分
平分![]() ,
,![]() 反向延长线交
反向延长线交![]() 延长线于
延长线于![]() ,若设
,若设![]() ,
,![]() ,试求
,试求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在等边△ABC中,D是边AC上一点,连接BD.将△BCD绕点B逆时针旋转60°得到△BAE,连接ED.若BC=10,BD=9,求△AED的周长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,半径均为1个单位长度的半圆O1,O2,O3,… 组成一条平滑的曲线,点P从原点O出发,沿这条曲线向右运动,速度为每秒![]() 个单位长度,则第2017秒时,点P的坐标是( )
个单位长度,则第2017秒时,点P的坐标是( )

A. (2016,0) B. (2017,-1) C. (2015,-1) D. (2017,1)
查看答案和解析>>
科目:初中数学 来源: 题型:
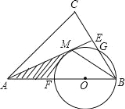
【题目】如图,在△ABC中,AB=AC,E是BC中点,点O在AB上,以OB为半径的⊙O经过点AE上的一点M,分别交AB,BC于点F,G,连BM,此时∠FBM=∠CBM.
(1)求证:AM是⊙O的切线;
(2)当BC=6,OB:OA=1:2 时,求![]() ,AM,AF围成的阴影部分面积.
,AM,AF围成的阴影部分面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,菱形ABCD的对角线AC与BD相交于点O,∠ABC∶∠BAD=1∶2,AC∥BE,CE∥BD.
(1)求∠DBC的度数;
(2)求证:四边形OBEC是矩形.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知MB=ND,∠MBA=∠NDC,下列哪个条件不能判定△ABM≌△CDN( )

A.AM=CNB.AB=CD C.AM∥CN D.∠M=∠N
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com