
ЁОЬтФПЁПДКНкЧАЃЌФГГЌЪаДгГЇМвЙКНјФГЩЬЦЗЃЌвбжЊИУЩЬЦЗУПИіЕФГЩБОМлЮЊ30дЊЃЌОЪаГЁЕїВщЗЂЯжЃЌИУЩЬЦЗУПЬьЕФЯњЪлСП![]() (Иі)гыЯњЪлЕЅМл
(Иі)гыЯњЪлЕЅМл![]() (дЊ) жЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЌЕБИУЩЬОЇУПИіЪлМлЮЊ40дЊЪБЃЌУПЬьПЩТєГі300ИіЃЛЕБИУЩЬОЇУПИіЪлМлЮЊ60дЊЪБЃЌУПЬьПЩТєГі100ИіЃЎ
(дЊ) жЎМфТњзувЛДЮКЏЪ§ЙиЯЕЃЌЕБИУЩЬОЇУПИіЪлМлЮЊ40дЊЪБЃЌУПЬьПЩТєГі300ИіЃЛЕБИУЩЬОЇУПИіЪлМлЮЊ60дЊЪБЃЌУПЬьПЩТєГі100ИіЃЎ
ЃЈ1ЃЉ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪНЮЊ__________________(ВЛвЊЧѓаДГі
жЎМфЕФКЏЪ§ЙиЯЕЪНЮЊ__________________(ВЛвЊЧѓаДГі![]() ЕФШЁжЕЗЖЮЇ) ЃЛ
ЕФШЁжЕЗЖЮЇ) ЃЛ
ЃЈ2ЃЉШєГЌЪаРЯАхЯыДяЕНУПЬьВЛЕЭгк220ИіЕФЯњЪлСПЃЌдђИУЩЬЦЗУПИіЪлМлЖЈЮЊЖрЩйдЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩйдЊ?
ЁОД№АИЁПЃЈ1ЃЉ![]() ЃЛЃЈ2ЃЉИУЩЬЦЗУПИіЪлМлЖЈЮЊ48дЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ3960дЊ
ЃЛЃЈ2ЃЉИУЩЬЦЗУПИіЪлМлЖЈЮЊ48дЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ3960дЊ
ЁОНтЮіЁП
(1)Щшy=kx+bЃЌдйИљОнУПИіЪлМлЮЊ40дЊЪБЃЌУПЬьПЩТєГі300ИіЃЛЕБИУЩЬОЇУПИіЪлМлЮЊ60дЊЪБЃЌУПЬьПЩТєГі100ИіЃЌСаЗНГЬзщЃЌДгЖјШЗСЂyгыxЕФКЏЪ§ЙиЯЕЮЊy=10x+700ЃЛ
(2)ЩшРћШѓЮЊWЃЌдђ![]() ЃЌНЋЦфЛЏЮЊЖЅЕуЪНЃЌгЩгкЖдГЦжсжБЯпВЛдк
ЃЌНЋЦфЛЏЮЊЖЅЕуЪНЃЌгЩгкЖдГЦжсжБЯпВЛдк![]() жЎМфЃЌгІЫЕУїКЏЪ§ЕФдіМѕадЃЌИљОнЕЅЕїадДњШыЧЁЕБздБфСПШЁжЕЃЌМДПЩЧѓГізюДѓжЕЃЎ
жЎМфЃЌгІЫЕУїКЏЪ§ЕФдіМѕадЃЌИљОнЕЅЕїадДњШыЧЁЕБздБфСПШЁжЕЃЌМДПЩЧѓГізюДѓжЕЃЎ
НтЃК(1)ЩшyгыxжЎМфЕФКЏЪ§НтЮіЪНЮЊy=kx+bЃЌ
гЩЬтвтЕУЃЌ![]() ЃЌ
ЃЌ
НтЕУЃК![]() ЃЌ
ЃЌ
ЁрyгыxжЎМфЕФКЏЪ§НтЮіЪНЮЊy=10x+700.
ЙЪД№АИЮЊ.![]()
(2)ЩшУПЬьЯњЪлРћШѓЮЊ![]() дЊЃЌгЩЬтвтЕУ
дЊЃЌгЩЬтвтЕУ
![]()
гЩгк![]() ЃЌЕУ
ЃЌЕУ![]()
Ёр![]()
гж![]() ЃЌЃЎЕБ
ЃЌЃЎЕБ![]() ЪБЃЌ
ЪБЃЌ ![]() ЫцзХ
ЫцзХ![]() ЕФдіДѓЖјдіДѓ
ЕФдіДѓЖјдіДѓ
ЁрЕБ![]() ЪБЃЌ
ЪБЃЌ![]() ШЁзюДѓжЕЃЌзюДѓжЕЮЊ
ШЁзюДѓжЕЃЌзюДѓжЕЮЊ![]()
Д№ЃКИУЩЬЦЗУПИіЪлМлЖЈЮЊ48дЊЪБЃЌУПЬьЕФЯњЪлРћШѓзюДѓЃЌзюДѓРћШѓЪЧ3960дЊ.



| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
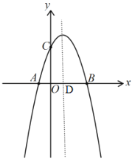
ЁОЬтФПЁПШчЭМЃЌЖўДЮКЏЪ§![]() ЕФЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЖдГЦжсгыxжсНЛгкЕуDЃЌШєЕуPЮЊyжсЩЯЕФвЛИіЖЏЕуЃЌСЌНгPDЃЌдђ
ЕФЭМЯѓгыxжсНЛгкAЃЌBСНЕуЃЌгыyжсНЛгкЕуCЃЌЖдГЦжсгыxжсНЛгкЕуDЃЌШєЕуPЮЊyжсЩЯЕФвЛИіЖЏЕуЃЌСЌНгPDЃЌдђ![]() ЕФзюаЁжЕЮЊ________.
ЕФзюаЁжЕЮЊ________.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПаЁУїМвЫљдкОгУёТЅЕФЖдУцгавЛзљДѓЯУABЃЌИпЮЊ74УзЃЌЮЊВтСПОгУёТЅгыДѓЯУжЎМфЕФОрРыЃЌаЁУїДгздМКМвЕФДАЛЇCДІВтЕУДѓЯУЖЅВПAЕФбіНЧЮЊ37ЁуЃЌДѓЯУЕзВПBЕФИЉНЧЮЊ48ЁуЃЎ
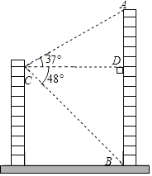
ЃЈ1ЃЉЧѓЁЯACBЕФЖШЪ§ЃЛ
ЃЈ2ЃЉЧѓаЁУїМвЫљдкОгУёТЅгыДѓЯУжЎМфЕФОрРыЃЎЃЈВЮПМЪ§ОнЃКsin37ЁуЁж![]() ЃЌcos37ЁуЁж
ЃЌcos37ЁуЁж![]() ЃЌtan37ЁуЁж
ЃЌtan37ЁуЁж![]() ЃЌsin48ЁуЁж
ЃЌsin48ЁуЁж![]() ЃЌcos48ЁуЁж
ЃЌcos48ЁуЁж![]() ЃЌtan48ЁуЁж
ЃЌtan48ЁуЁж![]() ЃЉ
ЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁП2019 ФъФГЪажэШтЪлМлж№дТЩЯеЧ,УПЧЇПЫжэШтЕФЪлМл![]() (дЊ)гыдТЗн
(дЊ)гыдТЗн![]() (
(![]() ,Чв
,Чв![]() ЮЊећЪ§)жЎМфТњзувЛДЮКЏЪ§ЙиЯЕ:
ЮЊећЪ§)жЎМфТњзувЛДЮКЏЪ§ЙиЯЕ:![]() ,УПЧЇПЫжэШтЕФГЩБО
,УПЧЇПЫжэШтЕФГЩБО![]() (дЊ)гыдТЗн
(дЊ)гыдТЗн![]() (
(![]() ,Чв
,Чв![]() ЮЊећЪ§)жЎМфТњзуЖўДЮКЏЪ§ЙиЯЕЃЌЧв3дТЗнУПЧЇПЫжэШтЕФГЩБОШЋФъзюЕЭЃЌЮЊ
ЮЊећЪ§)жЎМфТњзуЖўДЮКЏЪ§ЙиЯЕЃЌЧв3дТЗнУПЧЇПЫжэШтЕФГЩБОШЋФъзюЕЭЃЌЮЊ![]() дЊЃЌ
дЊЃЌ![]() дТЗнГЩБОЮЊ
дТЗнГЩБОЮЊ![]() дЊ.
дЊ.
ЃЈ1ЃЉЧѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪН;
жЎМфЕФКЏЪ§ЙиЯЕЪН;
ЃЈ2ЃЉЩшЯњЪлУПЧЇПЫжэШтЫљЛёЕУЕФРћШѓЮЊ![]() (дЊ),Чѓ
(дЊ),Чѓ![]() гы
гы![]() жЎМфЕФКЏЪ§ЙиЯЕЪН,ФФИідТЗнЯњЪлУПЧЇПЫжэШтЫљЛёЕУЕФРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩйдЊ?
жЎМфЕФКЏЪ§ЙиЯЕЪН,ФФИідТЗнЯњЪлУПЧЇПЫжэШтЫљЛёЕУЕФРћШѓзюДѓ?зюДѓРћШѓЪЧЖрЩйдЊ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
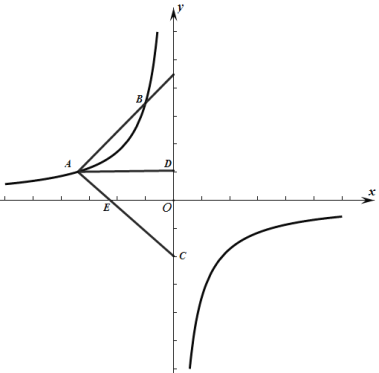
ЁОЬтФПЁПШчЭМЃЌЗДБШР§КЏЪ§![]() ЕФЭМЯѓОЙ§Еу
ЕФЭМЯѓОЙ§Еу![]() ЃЌЩфЯп
ЃЌЩфЯп![]() гыЗДБШР§КЏЪ§ЕФЭМЯѓЕФСэвЛИіНЛЕуЮЊ
гыЗДБШР§КЏЪ§ЕФЭМЯѓЕФСэвЛИіНЛЕуЮЊ![]() ,ЩфЯп
,ЩфЯп![]() гы
гы![]() жсНЛгкЕу
жсНЛгкЕу![]() ,гы
,гы![]() жсНЛгкЕу
жсНЛгкЕу![]() жсЃЌ ДЙзуЮЊ
жсЃЌ ДЙзуЮЊ![]() ЃЎ
ЃЎ
![]() ЧѓЗДБШР§КЏЪ§ЕФНтЮіЪН;
ЧѓЗДБШР§КЏЪ§ЕФНтЮіЪН;
![]() Чѓ
Чѓ![]() ЕФГЄ
ЕФГЄ
![]() дк
дк![]() жсЩЯЪЧЗёДцдкЕу
жсЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУ
ЃЌЪЙЕУ![]() гы
гы![]() ЯрЫЦЃЌШєДцдкЃЌЧыЧѓГіТњзуЬѕМўЕу
ЯрЫЦЃЌШєДцдкЃЌЧыЧѓГіТњзуЬѕМўЕу![]() ЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЌШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§yЃНmx2ЉЃЈ2m+1ЃЉx+2ЃЈmЁй0ЃЉЃЌЧыХаЖЯЯТСаНсТлЪЧЗёе§ШЗЃЌВЂЫЕУїРэгЩЃЎ
ЃЈ1ЃЉЕБmЃМ0ЪБЃЌКЏЪ§yЃНmx2ЉЃЈ2m+1ЃЉx+2дкxЃО1ЪБЃЌyЫцxЕФдіДѓЖјМѕаЁЃЛ
ЃЈ2ЃЉЕБmЃО0ЪБЃЌКЏЪ§yЃНmx2ЉЃЈ2m+1ЃЉx+2ЭМЯѓНиxжсЩЯЕФЯпЖЮГЄЖШаЁгк2ЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМЃЌЫФБпаЮABCDЪЧСтаЮЃЌЁЯA=60ЁуЃЌAB=2ЃЌЩШаЮBEFЕФАыОЖЮЊ2ЃЌдВаФНЧЮЊ60ЁуЃЌдђЭМжавѕгАВПЗжЕФУцЛ§ЪЧЃЈ ЃЉ

A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПФГЙЄГЇМЦЛЎЙКТђ![]() ЃЌ
ЃЌ![]() СНжжаЭКХЕФЛњЦїШЫМгЙЄСуМўЃЎвбжЊ
СНжжаЭКХЕФЛњЦїШЫМгЙЄСуМўЃЎвбжЊ![]() аЭЛњЦїШЫБШ
аЭЛњЦїШЫБШ![]() аЭЛњЦїШЫУПаЁЪБЖрМгЙЄ
аЭЛњЦїШЫУПаЁЪБЖрМгЙЄ![]() ИіСуМўЃЌЧв
ИіСуМўЃЌЧв![]() аЭЛњЦїШЫМгЙЄ
аЭЛњЦїШЫМгЙЄ![]() ИіСуМўгУЕФЪБМфгы
ИіСуМўгУЕФЪБМфгы![]() аЭЛњЦїШЫМгЙЄ
аЭЛњЦїШЫМгЙЄ![]() ИіСуМўЫљгУЕФЪБМфЯрЭЌЃЎ
ИіСуМўЫљгУЕФЪБМфЯрЭЌЃЎ
(1)Чѓ![]() ,
,![]() СНжжаЭКХЕФЛњЦїШЫУПаЁЪБЗжБ№МгЙЄЖрЩйСуМў;
СНжжаЭКХЕФЛњЦїШЫУПаЁЪБЗжБ№МгЙЄЖрЩйСуМў;
(2)ИУЙЄГЇМЦЛЎВЩЙК![]() ЃЌ
ЃЌ![]() СНжжаЭКХЕФЛњЦїШЫЙВ
СНжжаЭКХЕФЛњЦїШЫЙВ![]() ЬЈЃЌвЊЧѓУПаЁЪБМгЙЄСуМўВЛЕУЩйгк
ЬЈЃЌвЊЧѓУПаЁЪБМгЙЄСуМўВЛЕУЩйгк![]() ИіЃЌдђжСЩйЙКНј
ИіЃЌдђжСЩйЙКНј![]() аЭЛњЦїШЫЖрЩйЬЈ?
аЭЛњЦїШЫЖрЩйЬЈ?
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКГѕжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ1ЃЌвбжЊХзЮяЯп![]() гы
гы![]() жсНЛгк
жсНЛгк![]() ЃЌ
ЃЌ![]() СНЕуЃЌгы
СНЕуЃЌгы![]() жсНЛгк
жсНЛгк![]() ЕуЃЌЕу
ЕуЃЌЕу![]() ЪЧХзЮяЯпЩЯдкЕквЛЯѓЯоФкЕФвЛИіЖЏЕуЃЌЧвЕу
ЪЧХзЮяЯпЩЯдкЕквЛЯѓЯоФкЕФвЛИіЖЏЕуЃЌЧвЕу![]() ЕФКсзјБъЮЊ
ЕФКсзјБъЮЊ![]() ЃЎ
ЃЎ
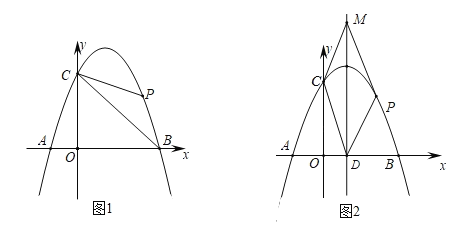
ЃЈ1ЃЉЧѓХзЮяЯпЕФБэДяЪНЃЛ
ЃЈ2ЃЉШчЭМ1ЃЌСЌНг![]() ЃЌ
ЃЌ![]() ЃЌ
ЃЌ![]() ЃЌЩш
ЃЌЩш![]() ЕФУцЛ§ЮЊ
ЕФУцЛ§ЮЊ![]() ЃЎЧѓ
ЃЎЧѓ![]() Йигк
Йигк![]() ЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіЕБ
ЕФКЏЪ§БэДяЪНЃЌВЂЧѓГіЕБ![]() ЮЊКЮжЕЪБЃЌ
ЮЊКЮжЕЪБЃЌ![]() ЕФУцЛ§
ЕФУцЛ§![]() газюДѓжЕЃЛ
газюДѓжЕЃЛ
ЃЈ3ЃЉШчЭМ2ЃЌЩшХзЮяЯпЕФЖдГЦжсЮЊжБЯп![]() ЃЌ
ЃЌ![]() гы
гы![]() жсЕФНЛЕуЮЊ
жсЕФНЛЕуЮЊ![]() ЃЎдкжБЯп
ЃЎдкжБЯп![]() ЩЯЪЧЗёДцдкЕу
ЩЯЪЧЗёДцдкЕу![]() ЃЌЪЙЕУЫФБпаЮ
ЃЌЪЙЕУЫФБпаЮ![]() ЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕу
ЪЧЦНааЫФБпаЮЃПШєДцдкЃЌЧѓГіЕу![]() ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ЕФзјБъЃЛШєВЛДцдкЃЌЧыЫЕУїРэгЩЃЎ
ВщПДД№АИКЭНтЮі>>
ЙњМЪбЇаЃгХбЁ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com