
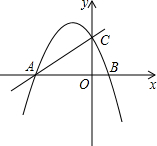
 (2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-
(2013•黄石)如图1所示,已知直线y=kx+m与x轴、y轴分别交于点A、C两点,抛物线y=-x2+bx+c经过A、C两点,点B是抛物线与x轴的另一个交点,当x=-| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| (x2-x1)2+(y2-y1)2 |
| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
| 1 |
| 2 |
| 25 |
| 4 |
| 1 |
| 2 |
| 25 |
| 4 |
 即A点坐标是(-3,0),B点坐标是(2,0).
即A点坐标是(-3,0),B点坐标是(2,0).
|
|
| ||
|
| 1 |
| 3 |
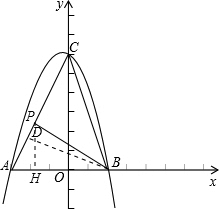 ∴AP:PC=1:3,
∴AP:PC=1:3,| OA2+OC2 |
| 5 |
| PH |
| OC |
| AP |
| AC |
| 1 |
| 4 |
| 3 |
| 2 |
| 3 |
| 2 |
| 9 |
| 4 |
| 9 |
| 4 |
| 3 |
| 2 |
 当点P在CA延长线时,作PG⊥x轴,点G为垂足.
当点P在CA延长线时,作PG⊥x轴,点G为垂足.| PG |
| OC |
| AP |
| AC |
| 1 |
| 2 |
| 9 |
| 2 |
| 9 |
| 2 |
| 9 |
| 4 |
| 3 |
| 2 |
| 9 |
| 2 |
| 1 |
| 2 |
|
|
|
| 3 |
| 2 |
| 3 |
| 2 |
| 3 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 4 |
| a |
| 2 |
| 1 |
| 4 |
| 3 |
| 4 |
 ①存在a的值,使得∠MON=90°.理由如下:
①存在a的值,使得∠MON=90°.理由如下:| x | 2 M |
| y | 2 M |
| x | 2 N |
| y | 2 N |
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |
| x | 2 M |
| y | 2 M |
| x | 2 N |
| y | 2 N |
| 1 |
| 4 |
| 3 |
| 4 |
| 5 |
| 2 |
| 5 |
| 2 |


 七彩题卡口算应用一点通系列答案
七彩题卡口算应用一点通系列答案科目:初中数学 来源: 题型:
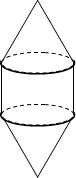 (2013•黄石)如图,已知某容器都是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成,若往此容器中注水,设注入水的体积为y,高度为x,则y关于x的函数图象大致是( )
(2013•黄石)如图,已知某容器都是由上下两个相同的圆锥和中间一个与圆锥同底等高的圆柱组合而成,若往此容器中注水,设注入水的体积为y,高度为x,则y关于x的函数图象大致是( )查看答案和解析>>
科目:初中数学 来源: 题型:
| AC |
| AB |
| BC |
| AC |
| S1 |
| S |
| S2 |
| S1 |

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com