练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    二次函数的图象如图所示，将其绕坐标原点O旋转，则旋转后的抛物线的解析式为(    ) 

    A．                 B．

    C．                     D．

     



    D

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    已知，相似比为3：1，且的周长为18，则的周长为            .             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在平面直角坐标系xOy中，AB在x轴上，以AB为直径的半⊙O’与y轴正半轴交于点C，连接BC，AC．CD是半⊙O’的切线，AD⊥CD于点D．

    （1）求证：∠CAD =∠CAB；

    （2）已知抛物线过A、B、C三点，AB=10 ，tan∠CAD=．

    ① 求抛物线的解析式；

       ② 判断抛物线的顶点E是否在直线CD上，并说明理由；

    ③ 在抛物线上是否存在一点P，使四边形PBCA是直角梯形．若存在，直接写出点P的坐标(不写求解过程)；若不存在，请说明理由．

    解：

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    画图：

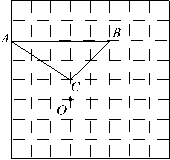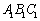    （1）如右图，已知△和点O．将△绕点O顺时针旋转90°得到△，在网格中画出△；

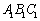    （2）如图，AB是半圆的直径，图1中，点C在半圆外；图2中，点C在半圆内，请仅用无刻度的直尺（只能画线）按要求画图．

       （i）在图1中，画出△的三条高的交点；

       （ii）在图2中，画出△中AB边上的高．

              

     


    图1                               图2

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图1，将两个完全相同的三角形纸片和重合放置，其中

    .

     


    （1）操作发现

    如图2，固定，使绕点顺时针旋转．当点恰好落在边上时，填空：

                                                    图1           图2

    ①     线段与的位置关系是          ；

    ②     设的面积为，的面积为，则与的数量关系是          ，证明你的结论；

    （2）猜想论证

        当绕点旋转到图3所示的位置时，小明猜想（1）中与的数量关系仍然成立，并尝试分别作出了和中BC，CE边上的高，请你证明小明的猜想．

                                                             

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    比较大小：      （填 “>”、“=”或“<”）．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知抛物线经过（0，-1），（3，2）两点．

    求它的解析式及顶点坐标．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    如图，在矩形ABCD中，AB=3，BC=4，点P在BC边上运动，连接DP，过点A作AE⊥DP，垂足为E，设DP=x，AE=y，则能反映y与x之间函数关系的大致图象是

     


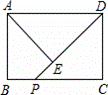
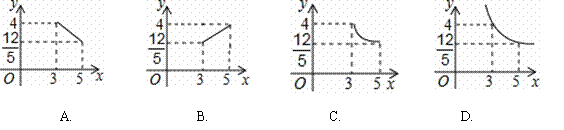
    查看答案和解析>>

    科目：初中数学 来源： 题型：


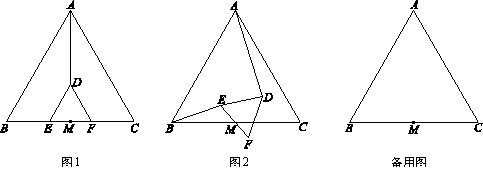
    已知：△ABC，△DEF都是等边三角形，M是BC与EF的中点，连接AD，BE.

    （1）如图1，当EF与BC在同一条直线上时，直接写出AD与BE的数量关系和位置关系；

    （2）△ABC固定不动，将图1中的△DEF绕点M顺时针旋转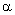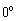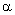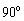（≤≤）角，如图2所示，判断（1）中的结论是否仍然成立，若成立，请加以证明；若不成立，说明理由；

    （3）△ABC固定不动，将图1中的△DEF绕点M旋转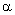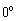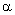（≤≤）角，作DH⊥BC于点H．设BH＝x，线段AB，BE，ED，DA所围成的图形面积为S．当AB＝6，DE＝2时，求S关于x的函数关系式，并写出相应的x的取值范围．

     


    查看答案和解析>>

    同步练习册答案