Question

如图，⊙O是△ABC的外接圆，AB=AC=10，BC=12，P是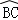上的一个动点，过点P作BC的平行线交AB的延长线于点D．

（1）当点P在什么位置时，DP是⊙O的切线？请说明理由；

（2）当DP为⊙O的切线时，求线段DP的长．

 

 

Answer 1

【答案】

解：（1）当点P是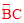的中点时，DP是⊙O的切线。理由如下：

连接AP。

∵AB=AC，∴。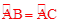

又∵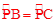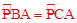，∴。∴PA是⊙O的直径。

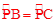∵，∴∠1=∠2。

又∵AB=AC，∴PA⊥BC。

又∵DP∥BC，∴DP⊥PA。∴DP是⊙O的切线。

（2）连接OB，设PA交BC于点E。．

 

 

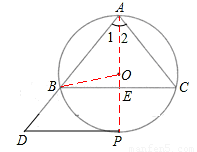
由垂径定理，得BE=BC=6。

在Rt△ABE中，由勾股定理，得：AE=。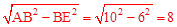

设⊙O的半径为r，则OE=8﹣r，

在Rt△OBE中，由勾股定理，得：r²=6²+（8﹣r）²，解得r=。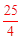

∵DP∥BC，∴∠ABE=∠D。

又∵∠1=∠1，∴△ABE∽△ADP，

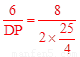∴，即，解得：。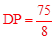

【解析】圆心角、弧、弦的关系，圆周角定理，切线的判定，勾股定理，垂径定理，相似三角形的判定和性质。

【分析】（1）根据当点P是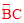的中点时，得出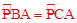，得出PA是⊙O的直径，再利用DP∥BC，得出DP⊥PA，问题得证。

（2）利用切线的性质，由勾股定理得出半径长，进而得出△ABE∽△ADP，即可得出DP的长。