
已知:抛物线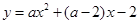 过点
过点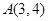 .
.
(1)求抛物线的解析式;
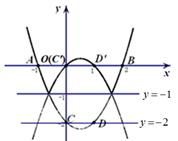
(2)将抛物线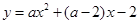 在直线
在直线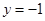 下方的部分沿直线
下方的部分沿直线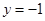 翻折,图象其余的部分保持不变,得到的新函数图象记为
翻折,图象其余的部分保持不变,得到的新函数图象记为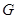 .点
.点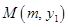 在图象
在图象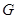 上,且
上,且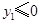 .
.
①求 的取值范围;
的取值范围;
②若点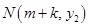 也在图象
也在图象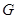 上,且满足
上,且满足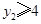 恒成立,则
恒成立,则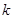 的取值范围为 .
的取值范围为 .
(1)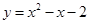 ;(2)①
;(2)①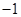 ≤
≤ ≤0或
≤0或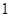 ≤
≤ ≤
≤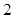 ;②
;②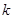 ≥4或
≥4或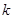 ≤
≤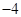 .
.
【解析】
试题分析:(1)由题意把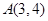 抛代入
抛代入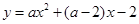 即可求得a的值,从而得到结果;
即可求得a的值,从而得到结果;
(2)①先求得(1)中的抛物线与x轴的交点坐标,再求得(1)中的抛物线与直线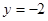 的交点坐标,即可得到关于直线
的交点坐标,即可得到关于直线 的对称点
的对称点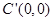 、
、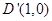 ,从而求得结果;②根据函数图象上的点的坐标的特征结合二次函数的性质求解即可.
,从而求得结果;②根据函数图象上的点的坐标的特征结合二次函数的性质求解即可.
(1)∵抛物线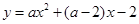 过点
过点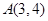 ,
,
∴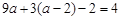 ,解得
,解得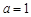 .
.
∴抛物线的解析式为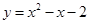 ;
;
(2)①当 时,
时,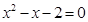 .
.
∴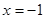 或
或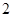 .
.
∴抛物线与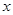 轴交于点
轴交于点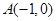 ,
,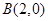
当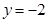 时,
时,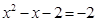 .
.
∴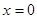 或
或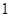 .
.
∴抛物线与直线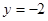 交于点
交于点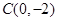 ,
, 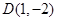 .
.
∴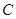 、
、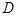 关于直线
关于直线 的对称点
的对称点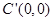 、
、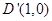 .
.
∴根据图象可得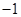 ≤
≤ ≤0或
≤0或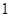 ≤
≤ ≤
≤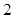 ;
;
②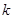 的取值范围为
的取值范围为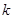 ≥4或
≥4或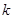 ≤
≤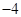 .
.
考点:二次函数的综合题
点评:此类问题综合性强,难度较大,在中考中比较常见,一般作为压轴题,题目比较典型.


科目:初中数学 来源: 题型:
 已知一抛物线过点O(0,0),A(6,0),B(4,3),
已知一抛物线过点O(0,0),A(6,0),B(4,3),查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知一抛物线过点O(0,0),A(6,0),B(4,3),
已知一抛物线过点O(0,0),A(6,0),B(4,3),查看答案和解析>>
科目:初中数学 来源:2009-2010学年天津市大港区九年级(上)期末数学试卷(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com