
【题目】如图,MN为一电视塔,AB是坡角为30°的小山坡(电视塔的底部N与山坡的坡脚A在同一水平线上,被一个人工湖隔开),某数学兴趣小组准备测量这座电视塔的高度.在坡脚A处测得塔顶M的仰角为45°;沿着山坡向上行走40m到达C处,此时测得塔顶M的仰角为30°,请求出电视塔MN的高度.(参考数据:![]() ≈1.41,
≈1.41,![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)

【答案】95m
【解析】过点C作CE⊥AN于点E, CF⊥MN于点F.在△ACE中,求AE=20![]() m,在RT△MFC中,设MN=x m,则AN=xm.FC=
m,在RT△MFC中,设MN=x m,则AN=xm.FC=![]() xm,可得x+20
xm,可得x+20![]() =
=![]() ( x-20),解方程可得答案..
( x-20),解方程可得答案..
解:过点C作CE⊥AN于点E, CF⊥MN于点F.
在△ACE中,AC=40m,∠CAE=30°
∴CE=FN=20m,AE=20![]() m
m
设MN=x m,则AN=xm.FC=![]() xm,
xm,
在RT△MFC中
MF=MN-FN=MN-CE=x-20
FC=NE=NA+AE=x+20![]()
∵∠MCF=30°
∴FC=![]() MF,
MF,
即x+20![]() =
=![]() ( x-20)
( x-20)
解得:x=![]()
=60+20![]() ≈95m
≈95m
答:电视塔MN的高度约为95m.



科目:初中数学 来源: 题型:
【题目】小明家、食堂、图书馆在同一条直线上.小明从家去食堂吃早餐,接着去图书馆读报,然后回家.下图反映了这个过程,小明离家的距离![]() 与时间
与时间![]() 之间的对应关系.根据图象,下列说法中正确的是( )
之间的对应关系.根据图象,下列说法中正确的是( )
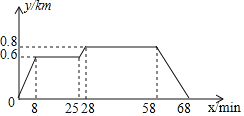
A. 小明吃早餐用了25分钟
B. 食堂到图书馆的距离为![]()
C. 小明读报用了30分钟
D. 小明从图书馆回家的平均速度为![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知抛物线![]() 的对称轴为直线
的对称轴为直线![]() ,且抛物线与
,且抛物线与![]() 轴交于
轴交于![]() 、
、![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,其中
点,其中![]() ,
,![]() .
.

(1)若直线![]() 经过
经过![]() 、
、![]() 两点,求直线
两点,求直线![]() 和抛物线的解析式;
和抛物线的解析式;
(2)在抛物线的对称轴![]() 上找一点
上找一点![]() ,使点
,使点![]() 到点
到点![]() 的距离与到点
的距离与到点![]() 的距离之和最小,求出点
的距离之和最小,求出点![]() 的坐标;
的坐标;
(3)设点![]() 为抛物线的对称轴
为抛物线的对称轴![]() 上的一个动点,求使
上的一个动点,求使![]() 为直角三角形的点
为直角三角形的点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在锐角△ABC中,AD是BC边上的高.∠BAF=∠CAG=90°,且AB=AF=AC=AG.连接FG,交DA的延长线于点E,连接BG,CF.下列结论:①∠FAG+∠BAC=180°;②BG=CF;③BG⊥CF;④∠EAF=∠ABC.其中一定正确的个数是( )
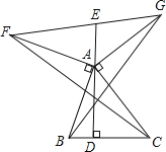
A.4个B.3个C.2个D.1个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在边长为1的小正方形网格中,△AOB的顶点均在格点上.
(1)B点关于y轴的对称点坐标为 ;
(2)将△AOB向左平移3个单位长度得到△A1O1B1,请画出△A1O1B1;
(3)在(2)的条件下,A1的坐标为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,AC=BC,点D在BC上,作∠ADF=∠B,DF交外角∠ACE的平分线CF于点F.

(1)求证:CF∥AB;
(2)若∠CAD=20°,求∠CFD的度数.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校八年级同学到距学校8千米的某地参加社会实践活动,一部分同学步行,另一部分同学骑自行车,沿相同路线前往.如图,![]() ,
,![]() 分别表示步行和骑车的同学前往目的地所走的路程
分别表示步行和骑车的同学前往目的地所走的路程![]() (千米)与所用时间
(千米)与所用时间![]() (分钟)之间的函数图象.则下列判断错误的是( )
(分钟)之间的函数图象.则下列判断错误的是( )
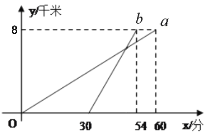
A. 骑车的同学比步行的同学晚出发30分钟
B. 骑车的同学和步行的同学同时到达目的地
C. 步行的速度是7.5千米/小时
D. 骑车的同学从出发到追上步行的同学用了18分钟
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,梯形ABCD中,AB∥CD,AB=24cm,DC=10cm,点P和Q同时从D、B出发,P由D向C运动,速度为每秒1cm,点Q由B向A运动,速度为每秒3cm,试求几秒后,P、Q和梯形ABCD的两个顶点所形成的四边形是平行四边形?
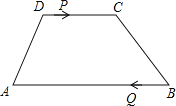
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某电器上销售一种微波炉和电磁炉,微波炉每台定价![]() 元,电磁炉每台定价
元,电磁炉每台定价![]() 元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;
元,“十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案;
方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的![]() 付款;
付款;
现某客户要到该卖场购买微波炉![]() 台,电磁炉
台,电磁炉![]() 台
台![]()
(1)若该客户按方案一、方案二购买,分别需付款多少元?(用含![]() 的式子表示)
的式子表示)
(2)若![]() ,通过计算说明此时那种方案购买较为核算?
,通过计算说明此时那种方案购买较为核算?
(3)当![]() 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法,并计算需付款多少元?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com