
【题目】如图,平面直角坐标系中,二次函数y=﹣![]() x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=
x2+bx+c的图线与坐标轴分别交于点A、B、C,其中点A(0,8),OB=![]() OA.
OA.
(1)求二次函数的表达式;
(2)若OD=OB,点F为该二次函数在第二象限内图象上的动点,E为DF的中点,当△CEF的面积最大时,求出点E的坐标;
(3)将三角形CEF绕E旋转180°,C点落在M处,若M恰好在该抛物线上,求出此时△CEF的面积.


【答案】(1)y=﹣![]() x2﹣x+8;(2)E(﹣
x2﹣x+8;(2)E(﹣![]() ,
,![]() );(3)
);(3)![]()
【解析】分析:(1)根据题意得出B点坐标,进而利用待定系数法求出函数解析式;
(2)首先求出直线DC的解析式进而表示出FP的长,再表示出S△CEF,进而得出E的坐标;
(3)根据题意表示出M点坐标,进而代入二次函数解析式得出m的值,即可得出答案.
详解:(1)∵OA=8,
∴OB=![]() OA=4,
OA=4,
∴B(4,0),
∵y=﹣![]() x2+bx+c的图象过点A(0,8),B(4,0),
x2+bx+c的图象过点A(0,8),B(4,0),
∴ ,解得:
,解得:![]() ,
,
∴二次函数表达式为:y=﹣![]() x2﹣x+8;
x2﹣x+8;
(2)当y=0时,﹣![]() x2﹣x+8=0,
x2﹣x+8=0,
解得:x1=4,x2=﹣8,
∴C点坐标为:(﹣8,0),
∵D点坐标为:(0,4),
∴设CD的解析为:y=kx+d,
故![]() ,解得:
,解得: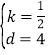 ,
,
故直线DC的解析为:y=![]() x+4;
x+4;
如图1,过点F作y轴的平行线交DC于点P,
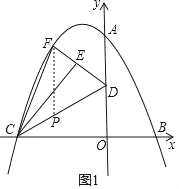
设F点坐标为:(m,﹣![]() m2﹣m+8),则P点坐标为:(m,
m2﹣m+8),则P点坐标为:(m,![]() m+4),
m+4),
则FP=﹣![]() m2﹣
m2﹣![]() m+4,
m+4,
∴S△FCD=![]() FPOC=
FPOC=![]() ×(﹣
×(﹣![]() m2﹣
m2﹣![]() m+4)×8
m+4)×8
=﹣m2﹣6m+16,
∵E为FD中点,
∴S△CEF=![]() ×S△FCD=﹣
×S△FCD=﹣![]() m2﹣3m+8=﹣
m2﹣3m+8=﹣![]() (m﹣3)2+
(m﹣3)2+![]() ,
,
当m=﹣3时,S△CEF有最大值,
∴﹣![]() m2﹣m+8=﹣
m2﹣m+8=﹣![]() ×9+3+8=
×9+3+8=![]() ,
,
E点纵坐标为:![]() ×(
×(![]() ﹣4)+4=
﹣4)+4=![]() ,
,
∴F(﹣3,![]() ),
),
∴E(﹣![]() ,
,![]() );
);
(3)如图2,∵F点坐标为:(m,﹣![]() m2﹣m+8),
m2﹣m+8),
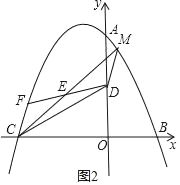
C点坐标为:(﹣8,0),D点坐标为:(0,4),
∴M(m+8,﹣![]() m2﹣m+12),
m2﹣m+12),
又∵M点在抛物线上,
∴﹣![]() (m+8)2﹣(m+8)+8=﹣
(m+8)2﹣(m+8)+8=﹣![]() m2﹣m+12,
m2﹣m+12,
解得:m=﹣7,
故S△CEF=﹣![]() m2﹣3m+8=
m2﹣3m+8=![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD为平行四边形纸片.把纸片ABCD折叠,使点B恰好落在CD边上,折痕为AF.且AB=10cm、AD=8cm、DE=6cm.
(1)求证:平行四边形ABCD是矩形;
(2)求BF的长;
(3)求折痕AF长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD中,AB∥DC,∠B=90°,F为DC上一点,且FC=AB,E为AD上一点,EC交AF于点G.
(1)求证:四边形ABCF是矩形;
(2)若EA=EG,求证:ED=EC.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,AB=AC,以AC为直径作⊙O交BC于点D,过点D作⊙O的切线,交AB于点E,交CA的延长线于点F.
(1)求证:EF⊥AB;
(2)若∠C=30°,EF=![]() ,求EB的长.
,求EB的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)|﹣2![]() |+|﹣3
|+|﹣3![]() |
|
(2)8.63﹣(﹣1.37)
(3)(﹣25)+34+156+(﹣65)
(4)(﹣0.5)﹣2![]() ﹣(+2
﹣(+2![]() )
)
(5)(﹣52)+24﹣(+74)+12.
(6)﹣![]() ﹣(﹣
﹣(﹣![]() )+(﹣
)+(﹣![]() )﹣(+
)﹣(+![]() )
)
(7)(+![]() )+(﹣
)+(﹣![]() )﹣(+
)﹣(+![]() )﹣(﹣
)﹣(﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知四边形 ABCD ,有以下四个条件:① AB ∥ CD ;② BC ∥ AD ;③ AB CD ;④ABC ADC .从这四个条件中任选两个,能使四边形 ABCD 成为平行四边形的选法有( )
A.3 种B.4 种C.5 种D.6 种
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,矩形ABCD中,AB=1,AD=2,点E是边AD上的一个动点,把△BAE沿BE折叠,点A落在A′处,如果A′恰在矩形的对称轴上,则AE的长为_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,所有小正方形的边长都为1个单位,A、B、C均在格点上.

(1)过点C画线段AB的平行线CD;
(2)过点A画线段BC的垂线,垂足为E;
(3)线段AE的长度是点 到直线 的距离;
(4)比较线段AE、AB、BC的大小关系(用“<”连接).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线![]() (a≠0)的对称轴为直
(a≠0)的对称轴为直![]() =1,与
=1,与![]() 轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:①
轴的一个交点坐标为(-1,0),其部分图象如图所示.下列结论:① ![]() ;②方程
;②方程![]() =0的两个根是
=0的两个根是![]() ,
,![]() ; ③
; ③![]() ;④当
;④当![]() 时,
时,![]() 的取值范围是
的取值范围是![]() ;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
;⑤当x1<x2<0时,y1<y2.其中结论正确的个数是( )
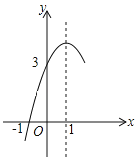
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com