
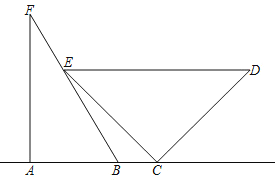
【题目】数学课上,静静将一幅三角板如图摆放,点![]() ,
,![]() ,
,![]() 三点共线,其中
三点共线,其中![]() ,
,![]() ,
,![]() ,且
,且![]() .
.
(1)若![]() ,
,![]() .求
.求![]() 的长.
的长.
(2)若![]() ,求
,求![]() 的长.
的长.
【答案】(1)![]() ;(2)2-
;(2)2-![]() .
.
【解析】
(1)在直角△AFB中,利用勾股定理求得AF的长度;
(2)如图,过点E作EG⊥AC于点G,构造等腰直角△EGC.在直角△EDC中,根据勾股定理求得EC的长度;然后在直角△EGC中,再次利用勾股定理求得GC的长度,在直角△EGB中,求得BG的长度,则BC=GC-GB.
(1)解:如图,直角△AFB中,∠FAB=90°,AB=2,BF=4.
由勾股定理知,AF=![]() ;
;
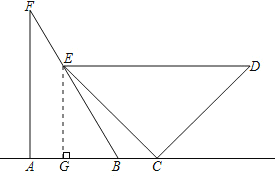
(2)解:如图,过点E作EG⊥AC于点G,则AF∥EG.
∵∠F=30°,
∴∠BEG=30°.
∴BG=![]() BE.
BE.
∵∠ECD=90°,∠D=45°,
∴∠DEC=∠D=45°.
∴EC=CD.
∴ED=![]() EC.
EC.
又ED=4,
∴EC=2![]() .
.
∵DE∥AC,
∴∠ECG=∠DEC=45°.
∴∠GEC=∠GCE=45°.
∴EG=CG.
∴EC=![]() GC,即2
GC,即2![]() =
=![]() GC.
GC.
∴GC=2.
在直角△BGE中,由勾股定理知BG2+EG2=BE2,即BG2+22=4BG2.
∴BG=![]() .
.
∴BC=GC-GB=2-![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】“龟兔首次赛跑”之后,输了比赛的兔子没有气馁,总结反思后,和乌龟约定再赛一场.图中的函数图象刻画了“龟兔再次赛跑”的故事(![]() 表示时间,
表示时间,![]() 、
、![]() 表示路程),根据图象解答下列问题:
表示路程),根据图象解答下列问题:
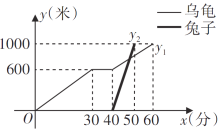
(1)“龟兔再次赛跑”的路程为__________米;
(2)它们两个约定__________先出发(填“兔子”和“乌龟”),先出发__________分钟;
(3)乌龟跑完全程用了__________分钟,兔子跑完全程用了__________分钟,乌龟平均速度是__________米/分,兔子平均速度是__________米/分;
(4)观察图象,你还能得出什么结论?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠A=90°,点D为BC的中点,DE⊥DF,DE交AB于点E,DF交AC于点F,试写出线段BE,EF,FC之间的数量关系,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
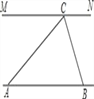
【题目】为解决江北学校学生上学过河难的问题,乡政府决定修建一座桥,建桥过程中需测量河的宽度(即两平行
河岸AB与MN之间的距离).在测量时,选定河对岸MN上的点C处为桥的一端,在河岸点A处,测得∠CAB=30°,
沿河岸AB前行30米后到达B处,在B处测得∠CBA=60°,请你根据以上测量数据求出河的宽度.(参考数据: ![]() ≈1.41,
≈1.41, ![]() ≈1.73,结果保留整数)
≈1.73,结果保留整数)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( )

A. 2 B. ![]() C.
C. ![]() D. 2
D. 2![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
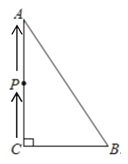
【题目】如图,△ABC中,![]() ,
,![]() ,
,![]() ,若点P从点C出发,以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动),设运动时间为t秒(
,若点P从点C出发,以每秒1cm的速度沿折线C→A→B→C运动(回到C点后点P停止运动),设运动时间为t秒(![]() ).
).
(1)若点P点AB边上,且满足![]() 时,求出此时t的值;
时,求出此时t的值;
(2)若点P恰好在∠BAC的角平分线上,求出此时t的值;
(3)在运动过程中,当△BCP为等腰三角形时,直接写出所有满足条件的t的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图①,在平面直角坐标系中,平行四边形ABCD在第一象限,且AB∥x轴.直线y=-x从原点出发沿x轴正方向平移,在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图②,那么平行四边形ABCD的面积为()
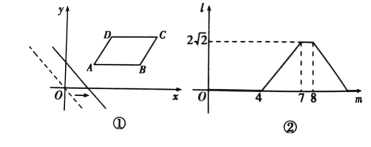
A.4B.![]() C.
C.![]() D.8
D.8
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com