
 ,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°.
,斜坡BD的长是50米,在山坡的坡底B处测得铁架顶端A的仰角为45°,在山坡的坡顶D处测得铁架顶端A的仰角为60°. ≈1.73,精确到0.1米)
≈1.73,精确到0.1米)
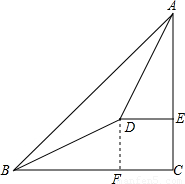 解:(1)如图,过D作DF垂直于坡底的水平线BC于点F.
解:(1)如图,过D作DF垂直于坡底的水平线BC于点F.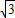 ,于是tan∠DBC=
,于是tan∠DBC= ,
,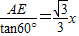 ,
,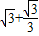 x,
x, x.
x. ≈43.3,即铁架高43.3米.
≈43.3,即铁架高43.3米.

科目:初中数学 来源:2006年全国中考数学试题汇编《二次函数》(10)(解析版) 题型:解答题
 ,0),B(-
,0),B(- ,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E. x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
查看答案和解析>>
科目:初中数学 来源:2009年浙江省杭州市高中招生学习能力数学模拟试卷(解析版) 题型:解答题
 ,0),B(-
,0),B(- ,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E. x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
查看答案和解析>>
科目:初中数学 来源:2006年湖南省常德市中考数学试卷(解析版) 题型:解答题
 ,0),B(-
,0),B(-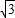 ,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E.
,0),以点A为圆心,AB为半径的圆与x轴相交于点B,C,与y轴相交于点D,E. x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
x2+bx+c经过C,D两点,求抛物线的解析式,并判断点B是否在该抛物线上;
查看答案和解析>>
科目:初中数学 来源:2011年山东省潍坊市中考数学模拟试卷(一)(解析版) 题型:选择题
 与⊙O的位置关系是( )
与⊙O的位置关系是( )
查看答案和解析>>
科目:初中数学 来源:2006年全国中考数学试题汇编《代数式》(05)(解析版) 题型:填空题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com