
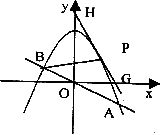
如图1,已知直线![]() 与抛物线
与抛物线![]() 交于
交于![]() 两点.
两点.
(1)求![]() 两点的坐标;
两点的坐标;
(2)求线段![]() 的垂直平分线的解析式;
的垂直平分线的解析式;
(3)如图2,取与线段![]() 等长的一根橡皮筋,端点分别固定在
等长的一根橡皮筋,端点分别固定在![]() 两处.用铅笔拉着这根橡皮筋使笔尖
两处.用铅笔拉着这根橡皮筋使笔尖![]() 在直线
在直线![]() 上方的抛物线上移动,动点
上方的抛物线上移动,动点![]() 将与
将与![]() 构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时
构成无数个三角形,这些三角形中是否存在一个面积最大的三角形?如果存在,求出最大面积,并指出此时![]() 点的坐标;如果不存在,请简要说明理由.
点的坐标;如果不存在,请简要说明理由.

答案:
解:(1)依题意得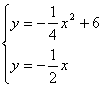 ,解
,解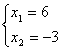 ;或
;或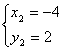 ,∴A(6,-3),B(-4,2),
,∴A(6,-3),B(-4,2),
(2)作AB的垂直平分线交![]() 轴,
轴,![]() 轴于C,D两点,交AB于M.
轴于C,D两点,交AB于M.
由(1)可知:OA=![]() 、OB=
、OB=![]() 。
。
∴AB=![]() 。∴
。∴![]() 。
。
过B作BE⊥![]() 轴,E为垂足。
轴,E为垂足。
由△BEO∽OMC,得:![]() ,
,
∴![]() ,同理:
,同理:![]() ,∴
,∴![]() ,
,![]() 。
。
设CD的解析式为![]() 。
。
∴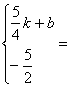 ∴
∴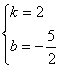
∴AB的垂直平分线的解析式为:![]()
(3)若存在点P使△APB的面积最大,则点P在与直线AB平行且和抛物线只有一个交点的直线![]() 上,并设该直线与
上,并设该直线与![]() 轴,
轴,![]() 轴交于G、H两点。
轴交于G、H两点。
∴
∴![]()
∵抛物线与直线只有一个交点,(可用![]() 转换)
转换)
∴![]() ,∴
,∴![]() 。∴
。∴![]() 。
。
在直线GH:![]() 中,
中,
∴![]() ,
,![]()
∴![]() 。设O到GH的距离为
。设O到GH的距离为![]() ,
,
∴![]() 。
。
∴![]() 。
。
∴![]()
∵AB∥GH,∴P到AB的距离等于O到GH的距离![]() 。
。
∴![]() 。
。



科目:初中数学 来源: 题型:
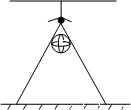
 如图,小明把小球竖直向上抛起,当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置,且灯与球心所在直线垂直于地面,这时小球在地面的影子的面积为1.92πm2.已知,灯与地面的距离为2.4m,小球的半径为
如图,小明把小球竖直向上抛起,当小球到达最高点时球的最高点正好处于距离屋顶白炽灯10cm的位置,且灯与球心所在直线垂直于地面,这时小球在地面的影子的面积为1.92πm2.已知,灯与地面的距离为2.4m,小球的半径为查看答案和解析>>
科目:初中数学 来源:101网校同步练习 初三数学 华东师大(新课标2001/3年初审) 华东师大版 题型:044
已知,如图,在平面直角坐标系xOy中,抛物线l1的解析式为y=-x2,将抛物线l1平移后得到抛线物l2,若抛物线l2经过点(0,2),且其顶点A的横坐标为最小正整数.

(1)求抛物线l2的解析式;
(2)说明将抛物线l1如何平移得到抛物线l2;
(3)若将抛物线l2沿其对称轴继续上下平移,得到抛物线l3,设抛物线l3的顶点为B,直线OB与抛物线l3的另一个交点为C.当OB=OC时,求点C的坐标.
查看答案和解析>>
科目:初中数学 来源:河南省期中题 题型:解答题
 中,抛物线
中,抛物线 的解析式为
的解析式为 ,将抛物线
,将抛物线 平移后得到抛线物
平移后得到抛线物 ,若抛物线
,若抛物线 经过点(0,2),且其顶点A的横坐标为最小正整数。
经过点(0,2),且其顶点A的横坐标为最小正整数。
查看答案和解析>>
科目:初中数学 来源: 题型:
如图所示,已知m、n是方程![]() 的两个实数根,且m<n,抛物线
的两个实数根,且m<n,抛物线![]() 的图像经过点A(m,0)、B(0,n).
的图像经过点A(m,0)、B(0,n).
 (1)求这个抛物线的解析式;
(1)求这个抛物线的解析式;
(2)设(1)中抛物线与x轴的另一交点为C,抛物线的
顶点为D,试求出点C、D的坐标和△BCD的面积;
(注:抛物线![]() 的顶点坐标为
的顶点坐标为
![]()
(3)P是线段OC上的一点,过点P作PH⊥x轴,与抛
物线交于H点,若直线BC把△PCH分成面积之比
为2:3的两部分,请求出P点的坐标.
查看答案和解析>>
科目:初中数学 来源:2012年湖北省荆州市沙市区中考数学综合练习卷(三)(解析版) 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com