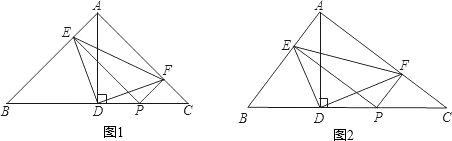
(1)证明:∵△ABC为等腰直角三角形,AD⊥BC,
∴AD=BD=CD,∠BAD=∠C=45°,
∵∠PEA=∠EAF=∠AFP=90°,
∴四边形AEPF是矩形,
∴AE=PF,
∵∠FPC=∠C=45°,
∴PF=CF,
∴AE=CF,
∴△ADE≌△CDF,
∴DE=DF,∠ADE=∠CDF;
又∵∠CDF+∠ADF=90°,
∴∠ADE+∠ADF=90°,
∴∠EDF=90°,
∴△DEF是等腰直角三角形;
∵△ABC为等腰直角三角形,
∴△DEF与△ABC相似.
(2)解:△DEF与△ABC仍相似,理由如下:
同(1)可知:四边形AEDF是矩形,则PF=AE;
∵∠PFC=∠ADC=90°,∠C公共,
∴△CFP∽△CAD,则有:

,
又∵∠EAD=∠FCD,
∴△FCD∽△EAD;
∴∠ADE=∠CDF,即∠EDF=90°;
且

;
又∵∠EDF=∠BAC,
∴△EDF∽△BAC.
(3)解:若△ABC是直角三角形,且AB=3,AC=4,则:
BC=5,S
△ABC=

AB•AC=6;
设CP=5x,依题意,则有:
CF=4x,PF=AE=3x,AF=AC-AF=4-4x;
在Rt△AEF中,由勾股定理得:
EF
2=AE
2+AF
2=9x
2+(4-4x)
2=25x
2-32x+16;
∵△DEF∽△ABC,
∴
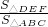
=(

)
2,即

=

;
∴S
△DEF=6x
2-

x+

=6(x-

)
2+

,
故当x=

,即CP=

时,△DEF的面积最小;
由于CD=
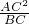
=

,所以当P运动到和D点重合时,△AEF的面积最小,且最小值为

.
分析:(1)若△ABC是等腰直角三角形,则△CPF也是等腰直角三角形,即CF=PF,易证得四边形PEAF是矩形,则CF=PF=AE,然后可证△ADE≌△CDF,通过全等三角形所得到的等角和等边,来证得△DEF是等腰直角三角形,由此说明△DEF与△ABC相似.
(2)题(1)的结论仍然成立,方法与(1)稍有不同,证全等改为证相似;由于PF⊥AC,易证得△CFP∽△CDA,得CF:PF=CD:AD,同(1)可证得PF=AE,即CF:AE=CD:AD,而它们的夹角∠EAD=∠FCD,由此可证得△CFD∽△AED,然后按照(1)的方法,根据相似三角形得到的等角和比例线段,来证得Rt△EDF∽Rt△BAC.
(3)欲求△DEF的面积最小值,需求得△DEF的面积表达式,设CP=5x,根据勾股定理易求得BC的长,那么即可用x表示出PF、CF的长,进而可得AE、AF的长,利用勾股定理可求出EF的表达式,(2)题中已证得△DEF∽△ABC,因此它们的面积比等于相似比的平方,△ABC的面积易求得,即可得到关于△DEF的面积和x的函数关系式,根据函数的性质即可求得△DEF的最小面积以及对应的x的值,由此可确定CP的长,即可判断出P点在线段BC上的位置.
点评:此题主要考查的是相似三角形的判定和性质;(2)题中,要根据两步相似来证所求的结论,(3)题中熟练掌握相似三角形的性质(相似三角形的面积比等于相似比的平方)是解决问题的关键.

 ,
, ;
; AB•AC=6;
AB•AC=6;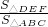 =(
=( )2,即
)2,即 =
= ;
; x+
x+ =6(x-
=6(x- )2+
)2+ ,
, ,即CP=
,即CP= 时,△DEF的面积最小;
时,△DEF的面积最小; =
= ,所以当P运动到和D点重合时,△AEF的面积最小,且最小值为
,所以当P运动到和D点重合时,△AEF的面积最小,且最小值为 .
.

 成功训练计划系列答案
成功训练计划系列答案 倍速训练法直通中考考点系列答案
倍速训练法直通中考考点系列答案 一卷搞定系列答案
一卷搞定系列答案 名校作业本系列答案
名校作业本系列答案 轻巧夺冠周测月考直通名校系列答案
轻巧夺冠周测月考直通名校系列答案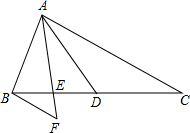 (2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.
(2012•松江区一模)已知:如图,在△ABC中,AD是边BC上的中线,点E在线段BD上,且BE=ED,过点B作BF∥AC,交线段AE的延长线于点F.