
【题目】如图,在直角坐标系中,矩形![]() 的顶点
的顶点![]() 与坐标原点重合,顶点
与坐标原点重合,顶点![]() 、
、![]() 分别在坐标轴上,顶点
分别在坐标轴上,顶点![]() 的坐标为
的坐标为![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点.
的中点.
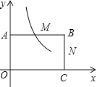
(1)若反比例函数![]() 的图象经过点
的图象经过点![]() ,求该反比例函数的解析式,并通过计算判断点
,求该反比例函数的解析式,并通过计算判断点![]() 是否在该函数的图象上;
是否在该函数的图象上;
(2)若反比例函数![]() 的图象与
的图象与![]() (包括边界)有公共点,请直接写出
(包括边界)有公共点,请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)反比例函数的解析式为![]() ,点
,点![]() 在函数
在函数![]() 的图象上;(2)
的图象上;(2)![]() .
.
【解析】
(1)根据顶点B的坐标为(4,2),M、N分别是AB、BC的中点.得到M点的坐标为(2,2),把M(2,2)代入反比例函数![]() (m≠0)可求出m,确定反比例函数的解析式;再根据B点坐标为(4,2),N点坐标为(4,1),易得N(4,1)满足反比例函数解析式,即可判断点N在该函数的图象上;
(m≠0)可求出m,确定反比例函数的解析式;再根据B点坐标为(4,2),N点坐标为(4,1),易得N(4,1)满足反比例函数解析式,即可判断点N在该函数的图象上;
(2)由反比例函数![]() (m≠0)的图象与△BMN的边始终有公共点,而M、N都在
(m≠0)的图象与△BMN的边始终有公共点,而M、N都在![]() 上,则此时m最小,反比例函数过B点时,m最大,此时m=4×2=8,由此得到m的取值范围.
上,则此时m最小,反比例函数过B点时,m最大,此时m=4×2=8,由此得到m的取值范围.
(1)∵顶点![]() 的坐标为
的坐标为![]() ,
,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,
的中点,
∴![]() 点的坐标为
点的坐标为![]() ,
,
把![]() 代入反比例函数
代入反比例函数![]() 得,
得,![]() ,
,
∴反比例函数的解析式为![]() ;
;
∵![]() 、
、![]() 分别为矩形
分别为矩形![]() 的边
的边![]() 、
、![]() 的中点,且
的中点,且![]() ,
,![]() 点坐标为
点坐标为![]() ,
,
∴![]() 点坐标为
点坐标为![]() ,
,
∵![]() ,
,
∴点![]() 在函数
在函数![]() 的图象上;
的图象上;
(2)![]() .
.


 初中学业考试导与练系列答案
初中学业考试导与练系列答案科目:初中数学 来源: 题型:
【题目】如图(1),在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点,点
的中点,点![]() ,
,![]() 分别在线段
分别在线段![]() ,
,![]() 上, 且
上, 且![]() .
.
(1)求证:![]() 为等腰直角三角形;
为等腰直角三角形;
(2)若![]() 的面积为7,求四边形
的面积为7,求四边形![]() 的面积;
的面积;
(3)如图(2),如果点![]() 运动到
运动到![]() 的延长线上时,点
的延长线上时,点![]() 在射线
在射线![]() 上且保持
上且保持![]() ,
,![]() 还是等腰直角三角形吗.请说明理由.
还是等腰直角三角形吗.请说明理由.


查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】等腰三角形的一个外角为100°,则这个等腰三角形的顶角为________;等腰三角形一腰上的高与腰的夹角为36°,则该等腰三角形的顶角为______.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为
为![]() 边上的中点.
边上的中点.
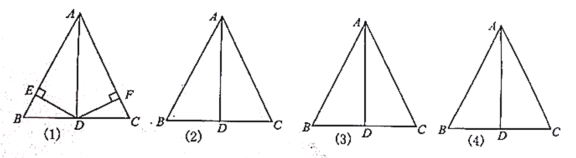
(1)若![]() 于
于![]() ,
,![]() 于
于![]() ,连接
,连接![]() .判断
.判断![]() 的形状,并证明;
的形状,并证明;
(2)若![]() 分别是
分别是![]() 上的中线,连接
上的中线,连接![]() .判断
.判断![]() 的形状,并说明理由;
的形状,并说明理由;
(3)若![]() 分别是
分别是![]() 的平分线,连接
的平分线,连接![]() .判断
.判断![]() 的关系,不需证明;
的关系,不需证明;
(4)若分别在![]() 上任取一点
上任取一点![]() ,且
,且![]() ,连接
,连接![]() .在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
.在不添加辅助线的情况下,你还能得到哪些不同于上面的正确结论?请写出至少四条,不需证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
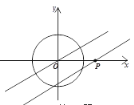
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,⊙O是以坐标原点为圆心,半径为1的圆,点P在
,⊙O是以坐标原点为圆心,半径为1的圆,点P在![]() 轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标为整数的点的个数有 _________个.
轴上运动,过点P且与直线l平行(或重合)的直线与⊙O有公共点,则点P的横坐标为整数的点的个数有 _________个.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在进行二次根式化简时,我们有时会碰上如![]() ,
,![]() ,
,![]() 一样的式子,这样的式子我们可以将其进一步化简
一样的式子,这样的式子我们可以将其进一步化简![]() =
=![]() ,
,![]() ,
,![]() 以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
以上这种化简的方法叫做分母有理化,请利用分母有理化解答下列问题:
(1)化简:![]() ;
;
(2)若a是![]() 的小数部分,求
的小数部分,求![]() 的值;
的值;
(3)矩形的面积为3![]() +1,一边长为
+1,一边长为![]() ﹣2,求它的周长.
﹣2,求它的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,正方形OABC的两边OA、OC分别在x轴、y轴上,点D(5,3)在边AB上,以C为中心,把△CDB旋转90°,则旋转后点D的对应点D′的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一般成年人的脚长(厘米)与鞋码(码)有如下关系:
脚长 | 23 | 23.5 | 24 | 24.5 | … |
鞋码 | 36 | 37 | 38 | 39 | … |
(1)若某人的脚长为26厘米,他应穿多少码的鞋?
(2)请建立鞋码![]() (厘米)与脚长
(厘米)与脚长![]() (码)之间的函数表达式;
(码)之间的函数表达式;
(3)我国著名篮球运动员姚明穿53码的鞋,请你根据以上关系计算他的脚长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com