
【题目】已知,在![]() 中,
中,![]() ,点
,点![]() 为边
为边![]() 上一动点,
上一动点,![]() 且
且![]() ,连接
,连接![]() ,其中
,其中![]() .
.
问题发现:(1)如图1,若![]() ,
,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?直接写出答案;
的值为多少?直接写出答案;
类比探究,(2)如图2,若![]() ,点
,点![]() 在
在![]() 的延长线上,
的延长线上,![]() 与
与![]() 有怎样的数量关系?
有怎样的数量关系?![]() 的值为多少?请说明理由.
的值为多少?请说明理由.
拓展应用:(3)如图3,在![]() 中,
中,![]() ,
,![]() ,
,![]() 为
为![]() 上一点,以
上一点,以![]() 为边,在如图所示位置作正方形
为边,在如图所示位置作正方形![]() ,点
,点![]() 为正方形
为正方形![]() 的对称中心,且
的对称中心,且![]() ,请直接写出
,请直接写出![]() 的长.
的长.

【答案】(1)∠BCE=∠A=60°;k=1;(2)∠BCE=∠A,k=![]() ,理由见解析;(3)
,理由见解析;(3)![]()
【解析】
(1)证明![]() ,得
,得![]() ,
,![]() 即可得解;
即可得解;
(2)先证明△ABC∽△DBE,![]() ,结合∠ABD=∠CBE,根据对应边成比例且夹角相等可证明△ABD∽△CBE,即可得出结论;
,结合∠ABD=∠CBE,根据对应边成比例且夹角相等可证明△ABD∽△CBE,即可得出结论;
(3)连接BO、OD,通过证明![]() ∽
∽![]() ,再根据相似三角形对应边成比例,求出DC,进而求出AD,再利用勾股定理求DB,则DE=DB.
,再根据相似三角形对应边成比例,求出DC,进而求出AD,再利用勾股定理求DB,则DE=DB.
解:(1)∵![]() ,
, ![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
又∵![]() 且
且![]() ,
,
∴![]() 为等边三角形,
为等边三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
在![]() 和
和![]() 中,
中,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴![]()
故答案为:![]() ,
,![]() .
.
(2)∠BCE=∠A,k=![]() .
.
理由如下:∵∠BAC=∠BDE,AB=AC,BD=DE,
∴∠ABC=∠DBE,
∴△ABC∽△DBE,
∴![]() ,
,
又∵∠ABC+∠CBD=∠DBE+∠CBD,即∠ABD=∠CBE
∴△ABD∽△CBE(对应边成比例,夹角相等),
∴![]() ,
,![]() ;
;
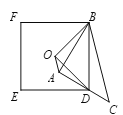
(3)如图,连接BO、OD,
∵四边形![]() 为正方形,点
为正方形,点![]() 为正方形
为正方形![]() 的对称中心,
的对称中心,
∴![]() ,
,![]() ,
,
∵![]() 为等腰直角三角形,
为等腰直角三角形,
∴![]() ,
,![]() ,
,
∴![]() ,
,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,
∴![]() ,
,
故![]() 的长为:
的长为:![]() .
.


 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案科目:初中数学 来源: 题型:
【题目】如图1,△ABC是等腰直角三角形,∠BAC= 90°,AB=AC,四边形ADEF是正方形,点B、C分别在边AD、AF上,此时BD=CF,BD⊥CF成立.

(1)当△ABC绕点A逆时针旋转θ(0°<θ<90°)时,如图2,BD=CF成立吗?若成立,请证明;若不成立,请说明理由.
(2)当△ABC绕点A逆时针旋转45°时,如图3,延长DB交CF于点H.
①求证:BD⊥CF;
②当AB=2,AD=3![]() 时,求线段DH的长.
时,求线段DH的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是抛物线y=ax2+bx+c(a≠0)的部分图象,其顶点坐标为(1,n),抛物线与x轴的一个交点在点(3,0)和(4,0)之间.则下列结论

①a-b+c>0;②3a+b=0;
③b2=4a(c-n);
④一元二次方程ax2+bx+c=n-1有两个不相等的实数根.
其中正确结论的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在抗击新型冠状病毒肺炎战役中,某市党员积极响应国家号召参加志愿者活动,为人民服务,现随机抽查部分党员一个月来参加志愿者活动的次数,并绘制成如下尚不完整的条形统计图(图1)和扇形统计图(图2).
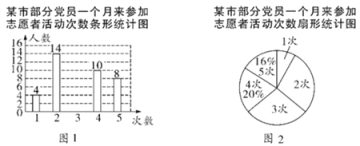
(1) “![]() 次”所在扇形的圆心角度数是 ,请补全 条形统计图;
次”所在扇形的圆心角度数是 ,请补全 条形统计图;
(2)若从抽在的党员中随机选择一位接受媒体的采访,求该党员一个月来参加志愿者活动次数不少于![]() 次的概率;
次的概率;
(3)设随机抽查的党员一个月来参加志愿者活动次数的中位数为![]() ,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为
,若去掉一部分党员参加志愿者活动的次数后,得到一组新数据的众数为![]() ,当
,当![]() 时,求最少去掉了几名党员参加志愿者活动的次数.
时,求最少去掉了几名党员参加志愿者活动的次数.
查看答案和解析>>
科目:初中数学 来源: 题型:
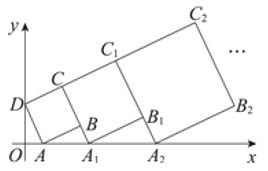
【题目】在平面直角坐标系中,正方形![]() 的位置如图所示,点
的位置如图所示,点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() ,延长
,延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;延长
;延长![]() 交
交![]() 轴于点
轴于点![]() ,作正方形
,作正方形![]() ;…,按照这样的规律作正方形,则点
;…,按照这样的规律作正方形,则点![]() 的纵坐标为__________.
的纵坐标为__________.
查看答案和解析>>
科目:初中数学 来源: 题型:
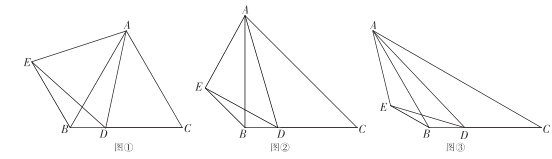
【题目】如图,在△ABC中, AB=AC,D 为 BC 边上任意一点,以AD为底边向左侧作等腰△ADE,∠AED=∠ABC ,连接![]() .
.
(1)如图 ① ,当∠ABC=60°时,易证:CD=BE(不需要证明);
(2)当∠ABC=90°时,如图 ② ;当∠ABC=120°时,如图 ③ ;线段CD和BE又有怎样的关系? 并选择一个图形证明你的结论.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下图是蜘蛛结网过程示意图,一只蜘蛛先以![]() 为起点结六条线
为起点结六条线![]() ,
,![]() 后,再从线
后,再从线![]() 上某点开始按逆时针方向依次在
上某点开始按逆时针方向依次在![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() …上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第2020个结点在( )
…上结网,若将各线上的结点依次记为1、2、3、4、5、6、7、8、…,那么第2020个结点在( )
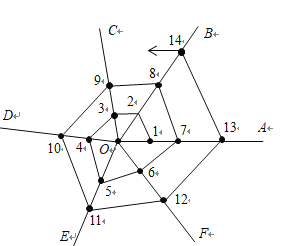
A.线![]() 上B.线OD上C.线OE上D.线
上B.线OD上C.线OE上D.线![]() 上
上
查看答案和解析>>
科目:初中数学 来源: 题型:
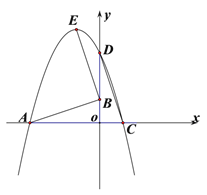
【题目】已知如图,抛物线![]() 与
与![]() 轴交于点A和点C(2,0),与
轴交于点A和点C(2,0),与![]() 轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
轴交于点D,将△DOC绕点O逆时针旋转90°后,点D恰好与点A重合,点C与点B重合.
(1)直接写出点A和点B的坐标;
(2)求![]() 和
和![]() 的值;
的值;
(3)已知点E是该抛物线的顶点,求证:AB⊥EB.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com