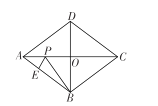
【题目】如图，菱形
的对角线交于点
是线段
上一动点， E 是线段 AB上一个动点，则
的最小值为 ____________．
【答案】
【解析】
本题中BP+EP是折线段，要想最小，故想办法将折线段拉直，故过B点作AC的对称点，刚好为D点，连接DP，则发现DP=BP，故相当于求DP+PE的最小值，根据点到直线的距离垂线段最短知：过D点作AB的垂线，交AB于H点，DH即为最小值，再利用菱形等面积法求DH的长.
解：过B点作AC的对称点，由菱形对称性知刚好落在D处，连接DP，
则BP=DP，故BP+EP=DP+EP，
过D点作DH⊥AB于H点，
∴ 当E、P、D三点共线，且DE⊥AB时，由点到直线的距离垂线段最短知：
此时DP+EP有最小值，为DH长.
又四边形ABCD为菱形，DH⊥AB，
∴由菱形的等面积法知：AB×DH=
×AC×BD，且AB=5，代入数据：
∴ 5×DH=×8×6，故DH=.
故答案为：.
名校课堂系列答案科目：初中数学 来源： 题型：
【题目】已知抛物线
．
（1）求抛物线
的开口方向、对称轴和顶点坐标；
（2）将抛物线向下平移，得抛物线
，使抛物线的顶点落在直线
上．
①求抛物线的解析式；
②抛物线与
轴的交点为
，
（点在点的左侧），抛物线的对称轴于轴的交点为
，点
是线段
上的一点，过点作直线
轴，交抛物线于点
，点关于抛物线对称轴的对称点为
，点
是线段
上一点，且
，连接
，作
交轴于点
，且
，求点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
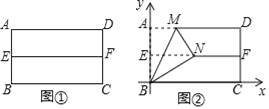
【题目】在我们学习过的数学教科书中，有一个数学活动，其具体操作过程是：
第一步：对折矩形纸片
，使
与
重合，得到折痕
，把纸片展开（如图①）；
第二步：再一次折叠纸片，使点
落在上，并使折痕经过点
，得到折痕
，同时得到线段
（如图②）．
如图②所示建立平面直角坐标系，请解答以下问题：
（Ⅰ）设直线的解析式为
，求
的值；
（Ⅱ）若
的延长线与矩形的边交于点
，设矩形的边
，
；
（i）若
，
，求点的坐标；
（ii）请直接写出
、
应该满足的条件．
查看答案和解析>>
科目：初中数学 来源： 题型：
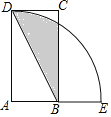
【题目】如图，四边形ABCD为矩形，以A为圆心，AD为半径的弧交AB的延长线于点E，连接BD，若AD=2AB=4，则图中阴影部分的面积为______．
查看答案和解析>>
科目：初中数学 来源： 题型：
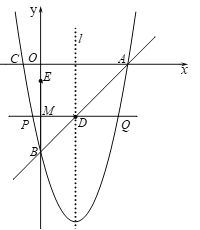
【题目】如图，直线
分别与
轴、
轴交于点
，抛物线
经过点，与轴的另一个交点为
，抛物线的对称轴
交
于点
．
（1）求抛物线的函数关系式及对称轴；
（2）若
为轴上一动点，
为
的中点，过点作的中垂线，交抛物线于点
，其中
在
的左边．
①如图1，若
时，求的长．
②当以点
为顶点的三角形是直角三角形时，请直接写出点的坐标．
查看答案和解析>>
科目：初中数学 来源： 题型：
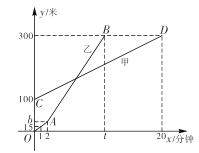
【题目】甲、乙二人都是户外运动爱好者，在一次登山活动中，甲、乙二人距出发点的高度
（单位：米），
（单位：米）与乙登山时间 x （单位：分钟）之间的函数图象如图所示，根据图象所提供的信息解答下列问题：
（1）甲登山的速度是每分钟 米，乙在 2 分钟时提速，提速时距地面的高度
为______米；
（2）若乙提速后，乙的速度是甲登山速度的 3 倍，请分别求出甲、乙二人登山全过程中，登山时距地面的高度 ， 与乙登山时间
之间的函数关系式；
（3）在（2）的条件下，乙登山多长时间追上了甲? 此时乙距提速时的高度为多少米?
查看答案和解析>>
科目：初中数学 来源： 题型：
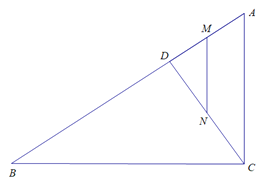
【题目】如图，在Rt⊿ABC中，∠ACB是直角， tan∠B=
,BC=16 cm,点D以2cm/s的速度由点A向点B匀速运动，到达点B即停止，M、N分别是AD、CD的中点，连结MN，设点D的运动时间为t
（1）求MN的长；
（2）求点D由点A到点B匀速运动过程中，线段MN所扫过的面积；
（3）若⊿DMN是等腰三角形时，求t的值．
查看答案和解析>>
科目：初中数学 来源： 题型：
【题目】南沙群岛是我国固有领土，现在我南海渔民要在南沙某海岛附近进行捕鱼作业，当渔船航行至B处时，测得该岛位于正北方向
海里的C处，为了防止某国还巡警干扰，就请求我A处的鱼监船前往C处护航，已知C位于A处的北偏东45°方向上，A位于B的北偏西30°的方向上，求A、C之间的距离．
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
