


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
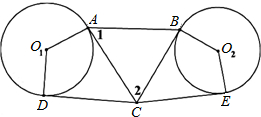
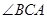 的顶点C,CA=CB.E、F分别是直线CD上两点,且
的顶点C,CA=CB.E、F分别是直线CD上两点,且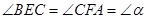 .
.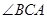 的内部,且E、F在射线CD上,请解决下面两个问题:
的内部,且E、F在射线CD上,请解决下面两个问题: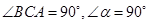 ,则
,则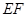
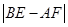 (填“
(填“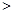 ”,“
”,“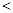 ”或“
”或“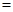 ”号);
”号);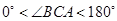 ,若使①中的结论仍然成立,则
,若使①中的结论仍然成立,则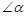 与
与 应满足的关系是 ;
应满足的关系是 ;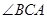 的外部,
的外部,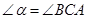 ,请探究EF、与BE、AF三条线段的数量关系,并给予证明.
,请探究EF、与BE、AF三条线段的数量关系,并给予证明.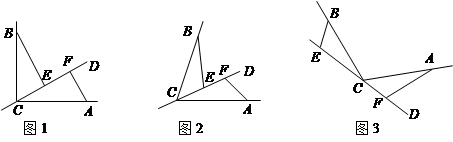
查看答案和解析>>
科目:初中数学 来源:2012届北京通州区中考模拟数学卷 题型:解答题
直线CD经过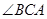 的顶点C,CA=CB.E、F分别是直线CD上两点,且
的顶点C,CA=CB.E、F分别是直线CD上两点,且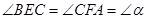 .
.
【小题1】若直线CD经过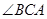 的内部,且E、F在射线CD上,请解决下面两个问题:
的内部,且E、F在射线CD上,请解决下面两个问题:
①如图1,若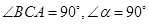 ,则
,则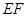
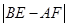 (填“
(填“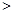 ”,“
”,“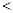 ”或“
”或“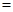 ”号);
”号);
②如图2,若 ,若使①中的结论仍然成立,则
,若使①中的结论仍然成立,则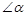 与
与 应满足的关系是 ;
应满足的关系是 ;
【小题2】如图3,若直线CD经过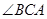 的外部,
的外部,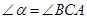 ,请探究EF、与BE、AF三条线段的数量关系,并给予证明.
,请探究EF、与BE、AF三条线段的数量关系,并给予证明.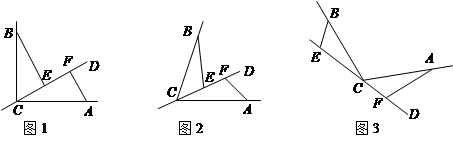
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com