
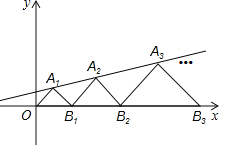
【题目】如图,在平面直角坐标系中,点![]() ,
,![]() ,
,![]() ,…和
,…和![]() ,
,![]() ,
,![]() ,…分别在直线
,…分别在直线![]() 和
和![]() 轴上.
轴上.![]() ,
,![]() ,
,![]() ,…都是等腰直角三角形,它们的面积分别记作
,…都是等腰直角三角形,它们的面积分别记作![]() ,
,![]() ,
,![]() ,…,如果点
,…,如果点![]() 的坐标为
的坐标为![]() ,那么
,那么![]() 的纵坐标为_______.
的纵坐标为_______.
【答案】![]()
【解析】
因为每个A点为等腰直角三角形的直角顶点,则每个点A的纵坐标为对应等腰直角三角形的斜边一半.故先设出各点A的纵坐标,可以表示A的横坐标,代入解析式可求点A的纵坐标,规律可求.
分别过点A1,A2,A3,…向x轴作垂线,垂足为C1,C2,C3,…
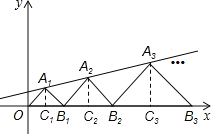
∵点A1(1,1)在直线y=![]() x+b上
x+b上
∴代入求得:b=![]()
∴y=![]() x+
x+![]()
∵△OA1B1为等腰直角三角形
∴OB1=2
设点A2坐标为(a,b)
∵△B1A2B2为等腰直角三角形
∴A2C2=B1C2=b
∴a=OC2=OB1+B1C2=2+b
把A2(2+b,b)代入y=![]() x+
x+![]()
解得b=![]()
∴OB2=5
同理设点A3坐标为(a,b)
∵△B2A3B3为等腰直角三角形
∴A3C3=B2C3=b
∴a=OC3=OB2+B2C3=5+b
把A3(5+b,b)代入y=![]() x+
x+![]()
解得b=![]()
以此类推,发现每个A的纵坐标依次是前一个的![]() 倍
倍
则A2019的纵坐标是(![]() )2019
)2019
故答案为:(![]() )2019
)2019


 考前必练系列答案
考前必练系列答案科目:初中数学 来源: 题型:
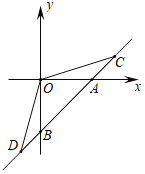
【题目】如图,直线l:y=x﹣2分别交x,y轴于A、B两点,C、D是直线l上的两个动点,点C在第一象限,点D在第三象限.且始终有∠COD=135°.
(1)求证:△OAC∽△DBO;
(2)若点C、D都在反比例函数y=![]() 的图象上,求k的值;
的图象上,求k的值;
(3)记△OBD的面积为S1,△AOC的面积为S2,且![]() =
=![]() ,二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当S1
,二次函数y=ax2+bx+c满足以下两个条件:①图象过C、D两点;②当S1![]() x
x![]() S2时,y有最大值2,求a的值.
S2时,y有最大值2,求a的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】每年夏天全国各地总有未成年人因溺水而丧失生命,令人痛心疾首.今年某中学为确保学生安全,开展了“远离溺水,真爱生命”的防溺水安全竞赛.学校对参加比赛的学生获奖情况进行了统计,绘制了如下两幅不完整的统计图,请结合图中相关数据解答下列问题.
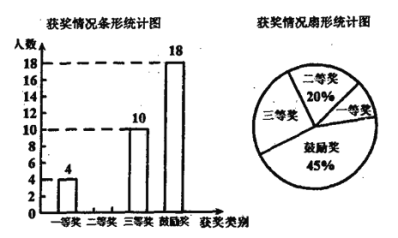
![]() 参加此安全竞赛的学生共有 人;
参加此安全竞赛的学生共有 人;
![]() 在扇形统计图中,“三等奖 ”所对应的扇形的圆心角的度数为 ;
在扇形统计图中,“三等奖 ”所对应的扇形的圆心角的度数为 ;
![]() 将条形统计图补充完整;
将条形统计图补充完整;
![]() 获得一等奖的学生中,
获得一等奖的学生中,![]() 人来自七年级,
人来自七年级,![]() 人来自八年级,
人来自八年级, ![]() 人来自九年级.学校决定从获得一等奖的学生中任选两名学生参加全市防漏水安全竞赛,请通过列表或树状图方法求所选两名学生中,恰好是一名七年级和一名九年级学生的概率.
人来自九年级.学校决定从获得一等奖的学生中任选两名学生参加全市防漏水安全竞赛,请通过列表或树状图方法求所选两名学生中,恰好是一名七年级和一名九年级学生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数![]() 的图像与反比例函数
的图像与反比例函数![]() 的图像交于
的图像交于![]() ,
,![]() 两点,与
两点,与![]() 轴分别交于
轴分别交于![]() 两点,且
两点,且![]() .
.
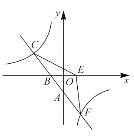
(1)求一次函数和反比例函数的解析式;
(2)若点![]() 与点
与点![]() 关于
关于![]() 轴对称,连接
轴对称,连接![]() ,求
,求![]() 的面积.
的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知![]() 是圆
是圆![]() 的直径,
的直径,![]() 是圆
是圆![]() 上一点,
上一点,![]() 的平分线交
的平分线交![]() 于点
于点![]() ,交
,交![]() 的切线
的切线![]() 于点
于点![]() ,过点
,过点![]() 作
作![]() ,交
,交![]() 的延长线于点
的延长线于点![]() .
.
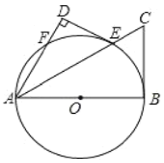
(1)求证:![]() 是
是![]() 的切线;
的切线;
(2)若![]() ,
,![]() ,
,
①求![]() 的值;②若点
的值;②若点![]() 为
为![]() 上一点,求
上一点,求![]() 最小值.
最小值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=x2+bx+c与x轴交于A(-1,0)、B(3,0)两点.
(1)求该抛物线的解析式;
(2)设(1)中的抛物线上有一个动点P,当点P在该抛物线上滑动到什么位置时,满足S△PAB=10,并求出此时P点的坐标;
(3)设(1)中的抛物线交y轴交于C点,在该抛物线的对称轴上是否存在点Q,使△QAC的周长最小?若存在,求出Q点的坐标;若不存在,请说明理由.
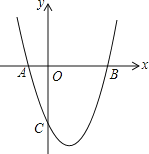
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,是全国最大的瓷碗造型建筑,座落于江西景德镇,整体造型概念来自“宋代影青斗笠碗”,造型庄重典雅,象征“万瓷之母”.小敏为了计算该建筑物横断面(瓷碗橫断面ABCD为等腰梯形)的高度,如图2,她站在与瓷碗底部AB位于同一水平面的点P处测得瓷碗顶部点D的仰角为45°,而后沿着一段坡度为0.44(坡面与水平线夹角的正切值)的小坡PQ步行到点Q(此过程中AD,AP,PQ始终处于同一平面)后测得点D的仰角减少了5°.已知坡面PQ的水平距离为20米,小敏身高忽略不计,试计算该瓷碗建筑物的高度.(参考数据:sin 40°≈0.64,tan 40°≈0.84)
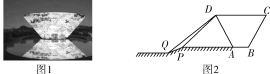
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() 为直径,
为直径,![]() 为弦.过
为弦.过![]() 延长线上一点
延长线上一点![]() ,作
,作![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,交
,交![]() 于点
于点![]() ,
,![]() 是
是![]() 的中点,连接
的中点,连接![]() ,
,![]() .
.
(1)判断![]() 与
与![]() 的位置关系,并说明理由;
的位置关系,并说明理由;
(2)若![]() ,
,![]() ,
,![]() ,求
,求![]() 的长.
的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个水库的水位在某段时间内持续上涨,表记录了连续5小时内6个时间点的水位高度,其中![]() 表示时间,
表示时间,![]() 表示水位高度.
表示水位高度.
| 0 | 1 | 2 | 3 | 4 | 5 | … |
| 3 | 3.3 | 3.6 | 3.9 | 4.2 | 4.5 | … |
(1)通过观察数据,请写出水位高度![]() (米)与时间
(米)与时间![]() (小时)的函数解析式(不需要写出定义域);
(小时)的函数解析式(不需要写出定义域);
(2)据估计,这种上涨规律还会持续,并且当水位高度达到8米时,水库报警系统会自动发出警报,请预测再过多久系统会发出警报.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com