
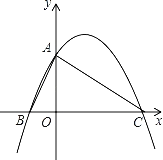
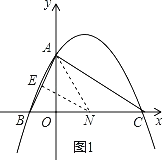
����Ŀ����ͼ�����κ���y��ax2+bx+c��a��0����ͼ����y�ύ�ڵ�A��0��4������x�Ḻ���ύ��B���������ύ�ڵ�C��8��0�����ҡ�BAC��90�㣮
��1����ö��κ�������ʽ��
��2����N���߶�BC��һ���㣬��NE��AC����AB�ڵ�E������AN������ANE������ʱ�����N�����ꣻ
��3������PΪx���Ϸ����������ϵ�һ�����㣬����PA��PC�������á�PAC�����ΪS���ʣ��Ƿ����һ��S��ֵ��ʹ����Ӧ�ĵ�P����ֻ��2�������У�������S��ֵ�������ʱ��P�ĺ����ꣻ�������ڣ���˵�����ɣ�
���𰸡���1��y����![]() x2+
x2+![]() x+4����2����3��0������3����S��16ʱ����Ӧ�ĵ�P����ֻ������
x+4����2����3��0������3����S��16ʱ����Ӧ�ĵ�P����ֻ������
��������
��1��֤��![]() �������B���꣬���ô���ϵ��������������κ�������ʽ��
�������B���꣬���ô���ϵ��������������κ�������ʽ��
��2����N��n��0������BN��n+2��BC��10��֤����BNE�ס�BAC���õ�S��BEN��![]() ��n+2��2�������S��BAN��2n+4�����ø�����
��n+2��2�������S��BAN��2n+4�����ø�����![]() �����ݶ��κ������ʼ�����⣻
�����ݶ��κ������ʼ�����⣻
��3����P![]() ���ֱ������0��m��8�ͩ�2��m��0ʱS��m������ϵʽ���������һ��S��ֵ��ʹ����Ӧ�ĵ�P����ֻ��2�����õ���S��16ʱ��m��4��m��
���ֱ������0��m��8�ͩ�2��m��0ʱS��m������ϵʽ���������һ��S��ֵ��ʹ����Ӧ�ĵ�P����ֻ��2�����õ���S��16ʱ��m��4��m��![]() ������������ý⣮
������������ý⣮
�⣺��1���ߡ�BAC��90�㣬��AOC=![]() ��90�㣬
��90�㣬
��![]()
![]()
![]()
![]()
��OA2��OBOC��
������֪��OA��4��OC��8��
��42��OB8��
��OB��2��
��B����2��0����
��A��B��C����������뼴�ã�
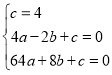 ��
��
��ã�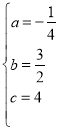 ��
��
�������߽���ʽΪ��y����![]() x2+
x2+![]() x+4��
x+4��
��2����N��n��0������BN��n+2��BC��10��
��NE��AC��
���BNE�ס�BAC��
��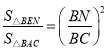 ��
��
��S��AC��![]() ��10��4��20��
��10��4��20��
��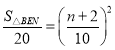 ��
��
S��BEN��![]() ��n+2��2��
��n+2��2��
��S��BAN��![]() ����n+2����4��2n+4��
����n+2����4��2n+4��
��![]() ��
��
��![]() ��
��
�൱n��3ʱ�����ֵS��ANE��5��
��ʱN������Ϊ����3��0����
��3����ֱ��AC��Ӧ�ĺ�������ʽΪ��y��kx+b��
��![]() ��
��
��ã�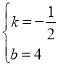 ��
��
��ֱ��AC��Ӧ�ĺ�������ʽΪ![]() ��
��
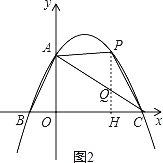
��ͼ����P��PH��OC������ΪH����ֱ��AC�ڵ�Q��
��P![]() ����Q
����Q![]() ��
��
�ٵ�0��m��8ʱ��
PQ![]() ��
��
S��S��APQ+S��CPQ��![]() ��8��
��8��![]() ������m��4��2+16��
������m��4��2+16��
��0��S��16��
�ڵ���2��m��0ʱ��
PQ����![]() ������
������![]() ����
����![]() ��
��
S��S��CPQ��S��APQ��![]() ��8����
��8����![]() ������m��4��2��16��
������m��4��2��16��
��0��S��20��
�൱0��S��16ʱ��0��m��8����m����ֵ����2��m��0��m��һ��ֵ����ʱ��������
��16��S��20ʱ����2��m��0��mֻ��һ��ֵ��
��S��16ʱ��m��4��m��![]() ��������
��������
�ʵ�S��16ʱ����Ӧ�ĵ�P����ֻ��������


 �Ͻ�ƽСѧ��������ϵ�д�
�Ͻ�ƽСѧ��������ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У���֪������![]() ��x�ύ�ڵ�
��x�ύ�ڵ�![]() ����
����![]() ����������y�ύ�ڵ�C������C�����ƶ�1����λ�õ���D��
����������y�ύ�ڵ�C������C�����ƶ�1����λ�õ���D��
��1���������߶Գ��
��2�����D�����꣨�ú���a�Ĵ���ʽ��ʾ����
��3����֪��![]() �������������߶�
�������������߶�![]() ֻ��һ�������㣬��a��ȡֵ��Χ��
ֻ��һ�������㣬��a��ȡֵ��Χ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ƽ��ֱ������ϵ�У�������![]() .... ����ͼ�ķ�ʽ���ã���
.... ����ͼ�ķ�ʽ���ã���![]()
![]() �͵�
�͵�![]() �ֱ�����ֱ��
�ֱ�����ֱ��![]() ��
��![]() ���ϣ�������
���ϣ�������![]() ����
����![]() ,�Ҷ�����ֱ��
,�Ҷ�����ֱ��![]() �ϣ�������
�ϣ�������![]() ����
����![]() ���Ҷ�����ֱ��
���Ҷ�����ֱ��![]() �ϣ�...���˹��ɣ�������
�ϣ�...���˹��ɣ�������![]() ,����
,����![]() , �Ҷ���Ҳ��ֱ��
, �Ҷ���Ҳ��ֱ��![]() �ϣ�����������
�ϣ�����������![]() ��������
��������![]() �ı�
�ı�![]() �ڵ�
�ڵ�![]() ��������
��������![]() ��������
��������![]() �ı�
�ı�![]() �ڵ�
�ڵ�![]() (����
(����![]() ��
��![]() ������) ��
������) ��

��1��ֱ��д�����е�����꣺![]() ��
��![]() ��
��
��2��д��������![]() �Ľ���ʽ����д��������
�Ľ���ʽ����д��������![]() �Ľ���ʽ�����̣��ٲ���������
�Ľ���ʽ�����̣��ٲ���������![]() �Ķ������ꣻ
�Ķ������ꣻ
��3����![]() �����ж�
�����ж�![]() ��
��![]() ��������ϵ��˵�����ɣ�
��������ϵ��˵�����ɣ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
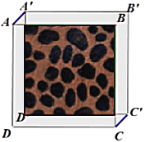
����Ŀ����ͼ������![]() ������ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ��õ�������
������ƽ��1����λ���ȣ�������ƽ��1����λ���ȣ��õ�������![]() ���γ����м���ɫ�������μ�����dzɫ�ı߿���֪������
���γ����м���ɫ�������μ�����dzɫ�ı߿���֪������![]() �����Ϊ16��������dzɫ�߿�������________��
�����Ϊ16��������dzɫ�߿�������________��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ,������ABCD��,AB=6,��DAB=60��,AE�ֱ�BC��BD�ڵ�E��F,��CE=2,����CF.���½���:�١�BAF=��BCF; �ڵ�E��AB�ľ�����2![]() ; ��S��CDF��S��BEF=9��4; ��tan��DCF=3/7. ������ȷ����()
; ��S��CDF��S��BEF=9��4; ��tan��DCF=3/7. ������ȷ����()
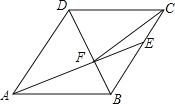
A. 4�� B. 3�� C. 2�� D. 1��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����ͼ���ڡ�ABC�У�AB=AC=5��BC=8��D��E�ֱ�ΪBC��AB����һ�㣬��ADE=��C��
��1����֤����BDE�ס�CAD��
��2����CD=2����BE�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������ϵ�з���һ����OABC����֪��ABC=60����OA=1���Ƚ�����OABC��x���������������ת��ÿ�η�ת60����������ת2020�Σ���B���������ΪB1��B2��B3��������B2020������Ϊ_________��
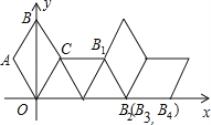
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ��AB�ǡ�O��ֱ���� OE��ֱ����BC������ΪF��OE����O�ڵ�D���ҡ�CBE=2��C��
��1����֤��BE���O���У�
��2����DF=9��tanC=![]() ����ֱ��AB�ij���
����ֱ��AB�ij���

�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����![]() �У�
�У�![]() ���ӳ�
���ӳ�![]() ʹ
ʹ![]() ���߶�
���߶�![]() �Ƶ�C˳ʱ����ת90���õ��߶�
�Ƶ�C˳ʱ����ת90���õ��߶�![]() ������
������![]() ��
��
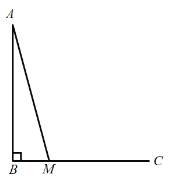
��1���������ⲹȫͼ�Σ�
��2����![]() ʱ��
ʱ��![]() �Ķ�����__________��
�Ķ�����__________��
��3��С��ͨ����ͼ���������֣���![]() ��һ������ʱ��
��һ������ʱ��![]() ��
��
С�ϰ���������ͬѧ�ǽ��н�����ͨ�����ۣ��γ���֤���ò���ļ����뷨��
�뷨1��ͨ���۲�ͼ�ο��Է��֣����������![]() ��ȫ��Ϊ������
��ȫ��Ϊ������![]() ������֤
������֤![]() ������õ�
������õ�![]() ������ֵʱ�������֤��
������ֵʱ�������֤��
�뷨2��Ҫ֤![]() ��ͨ���ڣ�2���ʣ���ֻ֪��Ҫ֤��
��ͨ���ڣ�2���ʣ���ֻ֪��Ҫ֤��![]() �ǵȱ������Σ�ͨ������ƽ���ı���
�ǵȱ������Σ�ͨ������ƽ���ı���![]() ����֤
����֤![]() ��ͨ��
��ͨ��![]() ����֤
����֤![]() ���Ӷ�������⣻
���Ӷ�������⣻
�뷨3��ͨ��![]() ������
������![]() ����֤
����֤![]() ����
����![]() �ǵ��������Σ���˵�
�ǵ��������Σ���˵�![]() ������ֵʱ�������֤��
������ֵʱ�������֤��
����ο�������뷨������С��֤����![]() ��һ������ʱ��
��һ������ʱ��![]() ����һ�ַ������ɣ�
����һ�ַ������ɣ�
�鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com